Fixed boundary tokamak equilibrium problem

The fixed boundary equilibrium problem (also called the ``inverse equilibrium problem'' by some authors) refers to the case where the shape of a magnetic surface is given and one is asked to solve the equilibrium within this magnetic surface. To make it convenient to deal with the shape of the boundary, one usually use a general coordinates system which has one coordinate surface coinciding with the given magnetic surface. This makes it trivial to deal with the irregular boundary. To obtain the equilibrium, one needs to solve the GS equation in the general coordinate system. Next we derive the form of the GS equation in a general coordinate system. The main task is to derive the form of the toroidal elliptic operator in the general coordinate system. The toroidal elliptic operator takes the form

$$\triangle^{\ast} \Psi \equiv R^2 \nabla \cdot \left( \frac{1}{R^2} \nabla \Psi \right)$$ (414)

For an arbitrary general coordinate system $(\psi , \theta , \phi )$ (the $(\psi , \theta , \phi )$ coordinate system here is an arbitrary general coordinate system except that $\nabla \phi$ is perpendicular to both $\nabla \psi$ and $\nabla \theta$), the toroidal elliptic operator is written

$$\triangle^{\star} \Psi = \frac{R^2}{\mathcal{J}} \left\{ \left[ \... ...frac{\mathcal{J}}{R^2} \nabla \theta \cdot \nabla \psi \right]_{\psi} \right\},$$ (415)

where the subscripts denotes partial derivatives, $\mathcal{J}$ is the Jacobian of the coordinate system $(\psi , \theta , \phi )$. [Next, we provide the proof of Eq. (415). The gradient of $\Psi$ is written as (note that $\Psi$ is independent of $\phi$)

$$\nabla \Psi = \frac{\partial \Psi}{\partial \theta} \nabla \theta + \frac{\partial \Psi}{\partial \psi} \nabla \psi,$$ (416)

which is in the covariant form. To calculate the divergence of $\nabla \Psi$, it is convenient to express $\nabla \Psi$ in terms of the contravariant basis vectors. Using the metric matrix, we obtain

$$\nabla \psi = \vert \nabla \psi \vert^2 \nabla \theta \times \nab... ...J}+ \nabla \psi \cdot \nabla \theta \nabla \phi \times \nabla \psi \mathcal{J},$$ (417)

and

$$\nabla \theta = \nabla \psi \cdot \nabla \theta \nabla \theta \ti... ...cal{J}+ \vert \nabla \theta \vert^2 \nabla \phi \times \nabla \psi \mathcal{J}.$$ (418)

Using these, Eq. (416) is written as

$$\nabla \Psi = \Psi_{\theta} (\nabla \psi \cdot \nabla \theta \nabla \theta \tim... ...J}+ \nabla \psi \cdot \nabla \theta \nabla \phi \times \nabla \psi \mathcal{J})$$

$$= (\Psi_{\theta} \nabla \psi \cdot \nabla \theta + \Psi_{\psi} \ver... ...si} \nabla \psi \cdot \nabla \theta) \nabla \phi \times \nabla \psi \mathcal{J}$$ (419)

Using the divergence formula, the elliptic operator in Eq. (414) is written as

$$\triangle^{\ast} \Psi = R^2 \nabla \cdot \left( \frac{1}{R^2} \nabla \Psi \right)$$

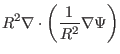$$= R^2 \nabla \cdot \left[ \frac{1}{R^2} (\Psi_{\theta} \nabla \psi ... ...la \psi \cdot \nabla \theta) \nabla \phi \times \nabla \psi \mathcal{J} \right]$$

$$= \frac{R^2}{\mathcal{J}} \left[ \frac{\partial}{\partial \psi} \le... ... \theta \vert^2 + \Psi_{\psi} \nabla \psi \cdot \nabla \theta) \right) \right],$$ (420)

$$= \frac{R^2}{\mathcal{J}} \left[ \left( \Psi_{\theta} \frac{\mathca... ...rac{\mathcal{J}}{R^2} \nabla \psi \cdot \nabla \theta \right)_{\theta} \right],$$

which is identical with Eq. (415).]

Using Eq. (415), the GS equation [Eq. (53)] is written

$$\frac{R^2}{\mathcal{J}} \left[ \left( \Psi_{\psi} \frac{\mathcal{... ...ight)_{\theta} \right] = - \mu_0 R^2 \frac{d P}{d \Psi} - \frac{d g}{d \Psi} g,$$ (421)

which is the form of the GS equation in $(\psi , \theta , \phi )$ coordinate system.