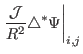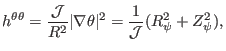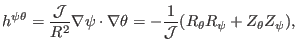The toroidal elliptic operator in Eq. (415) can be written
![$\displaystyle \triangle^{\ast} \Psi = \frac{R^2}{\mathcal{J}} [(h^{\psi \psi} \...
...^{\psi \theta} \Psi_{\theta})_{\psi} + (h^{\psi \theta} \Psi_{\psi})_{\theta}],$](img1288.png) |
(422) |
where
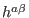 is defined by Eq. (174), i.e.,
is defined by Eq. (174), i.e.,
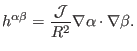 |
(423) |
Next, we derive the finite difference form of the toroidal elliptic operator.
The finite difference form of the term
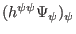 is
written
is
written
where
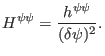 |
(425) |
The finite difference form of
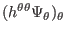 is
written
is
written
where
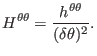 |
(427) |
The finite difference form of
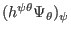 is
written as
is
written as
![$\displaystyle \left.(\Psi_{\theta} h^{\psi \theta})_{\psi} \right\vert _{i, j} ...
...i + 1, j - 1 / 2} - \Psi_{i - 1, j - 1 / 2}}{2 \delta \theta} \right) \right] .$](img1302.png) |
(428) |
Approximating the value of  at the grid centers by the average of the
value of
at the grid centers by the average of the
value of  at the neighbor grid points, Eq. (428) is written as
at the neighbor grid points, Eq. (428) is written as
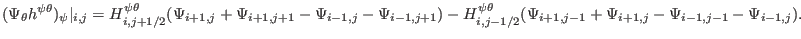 |
(429) |
where
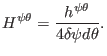 |
(430) |
Similarly, the finite difference form of
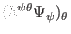 is written as
is written as
Using the above results, the finite difference form of the operator
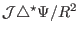 is written as
is written as
The coefficients are given by
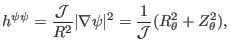 |
(432) |
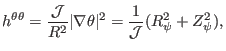 |
(433) |
and
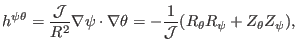 |
(434) |
where the Jacobian
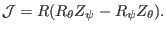 |
(435) |
The partial derivatives,
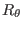 ,
, 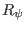 ,
,
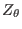 , and
, and
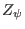 , appearing in Eqs. (432)-(435) are calculated by
using the central difference scheme. The values of
, appearing in Eqs. (432)-(435) are calculated by
using the central difference scheme. The values of
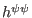 ,
,
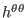 ,
,
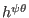 and
and
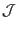 at the middle points are
approximated by the linear average of their values at the neighbor grid
points.
at the middle points are
approximated by the linear average of their values at the neighbor grid
points.
dd
yj
2018-03-09
![$\displaystyle \triangle^{\ast} \Psi = \frac{R^2}{\mathcal{J}} [(h^{\psi \psi} \...
...^{\psi \theta} \Psi_{\theta})_{\psi} + (h^{\psi \theta} \Psi_{\psi})_{\theta}],$](img1288.png)
![$\displaystyle \frac{1}{\delta
\psi} \left[ h^{\psi \psi}_{i, j + 1 / 2} \left( ...
... \psi} \left(
\frac{\Psi_{i, j} - \Psi_{i, j - 1}}{\delta \psi} \right) \right]$](img1293.png)
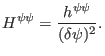
![$\displaystyle \frac{1}{\delta \theta} \left[ h^{\theta \theta}_{i + 1 / 2, j} \...
..., j} \left( \frac{\Psi_{i, j} - \Psi_{i - 1, j}}{\delta
\theta} \right) \right]$](img1298.png)
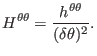
![$\displaystyle \frac{1}{\delta \theta} \left[ h^{\psi \theta}_{i + 1 / 2, j} \le...
...si_{i - 1 / 2, j +
1} - \Psi_{i - 1 / 2, j - 1}}{2 \delta \psi} \right) \right]$](img1307.png)