The function 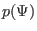 and
and 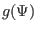 in the GS equation are free functions
which must be specified by users before solving the GS equation. Next, we
discuss one way to specify the free functions. Following Ref.
[9], we take
in the GS equation are free functions
which must be specified by users before solving the GS equation. Next, we
discuss one way to specify the free functions. Following Ref.
[9], we take 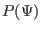 and
and 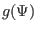 to be of the forms
to be of the forms
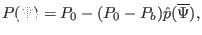 |
(441) |
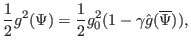 |
(442) |
with 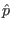 and
and 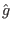 chosen to be of polynomial form:
chosen to be of polynomial form:
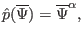 |
(443) |
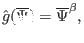 |
(444) |
where
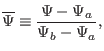 |
(445) |
with 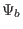 the value of
the value of  on the boundary,
on the boundary, 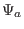 the value of
the value of
 on the magnetic axis,
on the magnetic axis,  ,
, 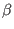 ,
, 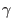 ,
, 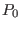 ,
, 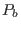 , and
, and
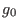 are free parameters. Using the profiles of
are free parameters. Using the profiles of 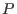 and
and 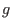 given by Eqs.
(441) and (442), we obtain
given by Eqs.
(441) and (442), we obtain
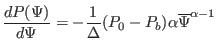 |
(446) |
where
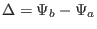 , and
, and
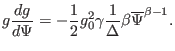 |
(447) |
Then the term on the r.h.s (nonlinear source term) of the GS equation is
written
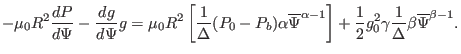 |
(448) |
The value of parameters 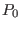 ,
, 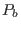 , and
, and 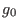 in Eqs. (441) and
(442), and the value of
in Eqs. (441) and
(442), and the value of  and
and 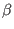 in Eqs. (443)
and (444) can be chosen arbitrarily. The parameter
in Eqs. (443)
and (444) can be chosen arbitrarily. The parameter 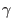 is used to
set the value of the total toroidal current. The toroidal current density is
given by Eq. (62), i.e.,
is used to
set the value of the total toroidal current. The toroidal current density is
given by Eq. (62), i.e.,
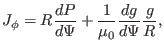 |
(449) |
which can be integrated over the poloidal cross section within the boundary
magnetic surface to give the total toroidal current,
Using
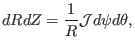 |
(451) |
Eq. (450) is written as
![$\displaystyle I_{\phi} = \int \left[ \left( - \frac{1}{\Delta} \right) (P_0 - P...
...\frac{1}{\Delta} \hat{g}' (\overline{\Psi}) \right] \mathcal{J}d \psi d \theta,$](img1358.png) |
(452) |
from which we solve for 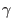 , giving
, giving
![$\displaystyle \gamma = \frac{- \Delta I_{\phi} - (P_0 - P_b) \int [\hat{p}' (\o...
... \frac{1}{R^2} \hat{g}' (\overline{\Psi}) \right] \mathcal{J}d \psi d \theta} .$](img1359.png) |
(453) |
If the total toroidal current 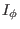 is given, Eq. (453) can be
used to determine the value of
is given, Eq. (453) can be
used to determine the value of 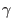 .
.
yj
2018-03-09
![]() and
and ![]() in the GS equation are free functions
which must be specified by users before solving the GS equation. Next, we
discuss one way to specify the free functions. Following Ref.
[9], we take
in the GS equation are free functions
which must be specified by users before solving the GS equation. Next, we
discuss one way to specify the free functions. Following Ref.
[9], we take ![]() and
and ![]() to be of the forms
to be of the forms
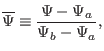
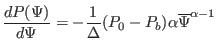
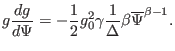
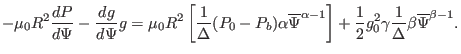
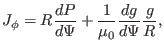
![$\displaystyle I_{\phi} = \int \left[ \left( - \frac{1}{\Delta} \right) (P_0 - P...
...\frac{1}{\Delta} \hat{g}' (\overline{\Psi}) \right] \mathcal{J}d \psi d \theta,$](img1358.png)