Fixed boundary equilibrium numerical code

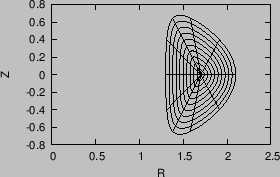
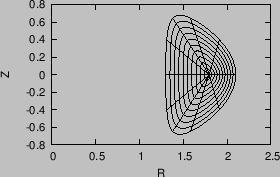
The tokamak equilibrium problem where the shape of the LCFS is given is called fixed boundary equilibrium problem. I wrote a numerical code that uses the iterative metric method[7] to solve this kind of equilibrium problem. Figure 30 describes the steps involved in the iterative metric method.

Figure 30: Upper left figure plots the initial coordinate surfaces. After solving the GS equation to obtain the location of the magnetic axis, I shift the origin point of the initial coordinate system to the location of the magnetic axis (upper right figure). Then, reshape the coordinate surface so that the coordinate surfaces $\psi = \ensuremath {\operatorname {const}}$ lies on magnetic surfaces (middle left figure). Recalculate the radial coordinate $\psi$ that is consistent with the Jacobian constraint and interpolate flux surface to uniform $\psi$ coordinates (middle right figure). Recalculate the poloidal coordinate $\theta$ that is consistent with the Jacobian constraint and interpolate poloidal points on every flux surface to uniform $\theta$ coordinates (bottom left figure).