Next: Low-beta equilibrium vs. high-beta Up: Special treatment at coordinate Previous: Fixed boundary equilibrium numerical
To benchmark the numerical code, I set the profile of ![]() and
and ![]() according to
Eqs. (69) and (70) with the parameters
according to
Eqs. (69) and (70) with the parameters ![]() ,
,
![]() ,
,
![]() , and
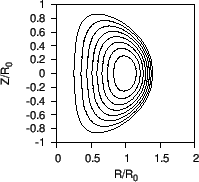
, and ![]() . The comparison of the analytic and numerical results are shown in Fig.
31.
. The comparison of the analytic and numerical results are shown in Fig.
31.
 |
Note that the parameter ![]() in the Solovev equilibrium seems to be not
needed in the numerical calculation. In fact this impression is wrong: the
in the Solovev equilibrium seems to be not
needed in the numerical calculation. In fact this impression is wrong: the
![]() parameter is actually needed in determining the boundary magnetic
surface of the numerical equilibrium (in the case considered here
parameter is actually needed in determining the boundary magnetic
surface of the numerical equilibrium (in the case considered here ![]() is
chosen as
is
chosen as
![]() ).
).