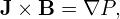
The MHD momentum equation of plasmas is given by
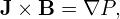 | (55) |
where ρ, ρq, ℙ, J, E, and B are mass density, charge density, thermal pressure tensor, current density, electric field, and magnetic field, respectively. The electric field force ρqE is usually ignored due to either ρq = 0 or E = 0. Further assume that there is no plasma flow (u = 0, the flow effect is discussed in A.2) and the plasma pressure is isotropic, then the steady state momentum equation (force balance equation) is written
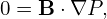 | (56) |
where P is the scalar plasma pressure.
Is the force balance (56) always satisfied in a real toakamak discharge? To answer this question, we need to go back to the original momentum equation (55). The imbalance between J × B and ∇P will give rise to the compressional Alfven waves, the time-scale of which, τA, is much shorter than the time-scale τ we are interested in. Therefore, on the time scale τ and for slow flow with u < Cs, where Cs is the the sound speed, the leading order of the momentum equation is the force balance (56). (to be sure, I need to think about this again). This reasoning is from Youwen Sun[24].