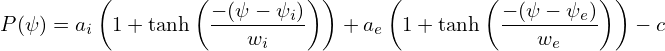[next] [prev] [prev-tail] [tail] [up]

A.2 Plasma rotation

In deriving the Grad-Shafranov equation, we have assumed that there is no plasma flow. Next, let us examine whether this assumption is justified for plasmas in EAST tokamak.

The complete momentum equation is given by

[ ] ρm ∂U- + U ⋅∇U = ρqE + J ×B − ∇ ⋅ℙ, ∂t
(526)

where ρqE term can be usually neglected due to either ρq ≈ 0 or E ≈ 0, ℙ is a pressure tensor, which is different from the scalar pressure considered in this note. The equilibrium with pressure tensor can be important for neutral beam heating plasma, where pressure contributed by NBI fast ions can be a tensor. With plasma flow and scalar pressure and neglecting electric force term, the steady state momentum equation is written

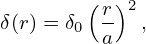ρmU ⋅∇U = J× B − ∇P,
(527)

where the term on the left-hand side is the contribution of plasma flow to the force balance. Let us estimate the magnitude of this term. Macroscopic flows in tokamak are usually along the toroidal direction (the poloidal flow is usually heavily damped). The toroidal flow usually has the same toroidal angular frequency on a magnetic surface, i.e., the flow can be written as

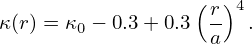U = R ωT(ψ)eϕ,
(528)

where ωT = ωT(ψ) is the toroidal angular frequency of the flow, which can have radial variation. Using this expression, the left-hand side of Eq. (527) is written as

ρmU ⋅∇U = ρmR ωTeϕ ⋅∇(RωT eϕ) -1-∂- = ρmR ωTR ∂ ϕ(RωTeϕ) = − ρmR ω2 eR, (529) T
which is just the centripetal force. For typical EAST plasma, the rotation frequency fT = ωT∕2π is less than 10kHz. For fT = 10kHz, R = 1.8m and ρm = 1.3 × 10−7 kg ∕m3 [Mass density of EAST#38300@3.9s, ρm = nDmD = 4 × 1019m−3 × 2 × 1.6726 × 10−27 kg = 1.3 × 10−7 kg ∕m3], the above fore is about 9.23 × 102 newton. On the other hand, the pressure gradient force in Eq. (527) is about 4 × 104 newton, which is one order larger than the force contributed by the rotation. [Pressure gradient force is estimated by using ∇P ≈ P0∕a, where P0 is the thermal pressure at the magnetic axis and a is the minor radius of plasma. For typical EAST plasmas (EAST#38300@3.9s), P0 ≈ 2 × 104 Pa, a = 0.45m. Then ∇P ≈ P0∕a = 4 × 104N∕m3.]  This indicates the rotation has little influence on the force balance. In other words, the EAST tokamak equilibrium can be well described by the static equilibrium without rotation.

[next] [prev] [prev-tail] [front] [up]