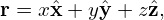
In the Cartesian coordinates, a point is described by its coordinates (x,y,z), which, in the vector form, is written as
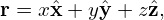 | (74) |
where r is the location vector of the point; 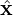 ,
, 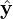 , and
, and 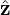 are the basis vectors of the Cartesian
coordinates, which are constant, independent of spactial location. The transformation between the
Cartesian coordinates system, (x,y,z), and a general coordinates system, (x1,x2,x3), can be expressed
as
are the basis vectors of the Cartesian
coordinates, which are constant, independent of spactial location. The transformation between the
Cartesian coordinates system, (x,y,z), and a general coordinates system, (x1,x2,x3), can be expressed
as
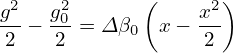 | (75) |
For example, cylindrical coordinates (R,ϕ,Z) can be considered as a general coordinate systems, which
are defined by r = R cosϕ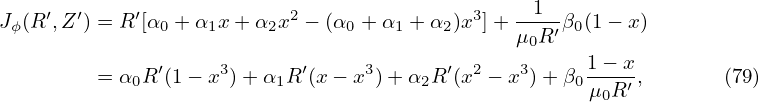 + R sinϕ
+ R sinϕ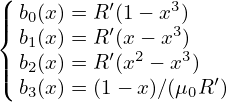 + Z
+ Z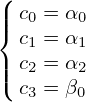 .
.
The transformation function in Eq. (75) can be written as
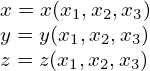 | (76) |