[next] [prev] [prev-tail] [tail] [up]

6.2 Jacobian

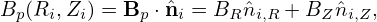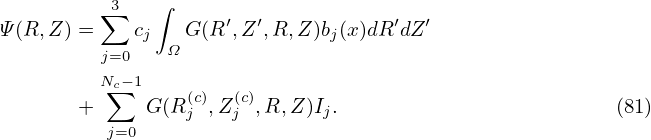
A useful quality characterizing coordinate transformation is the Jacobian determinant (or simply called Jacobian), which, for the transformation in Eq. (76), is defined by

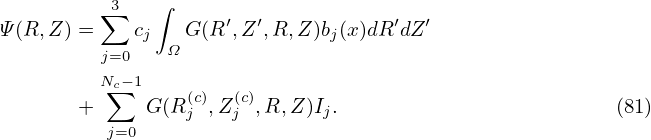| | || ∂∂xx-∂∂xx- ∂∂xx-|| 𝒥 = || ∂1y-∂y2 ∂3y-||, || ∂x∂1z-∂∂xz2 ∂x∂3z-|| ∂x1 ∂x2 ∂x3
(77)

which can also be written as

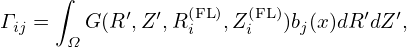∂r ∂r ∂r 𝒥 = ∂x-× ∂x--⋅∂x--. 1 2 3
(78)

It is easy to prove that the Jacobian 𝒥 in Eq. (78) can also be written (the derivation is given in my notes on Jacobian)

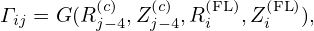−1 𝒥 = (∇x1 × ∇x2 ⋅∇x3 ) .
(79)

Conventionally, the Jacobian of the transformation from the Cartesian coordinates to a particular coordinate system σ is called the Jacobian of σ, without explitly mentioning that this transformation is with respect to the Cartesian coordinates.

Using the defintion in Eq. (77), the Jacobian 𝒥 of the Cartesian coordinates can be calculated, yielding 1. Likewise, the Jacobian of the cylindrical coordinates (R,ϕ,Z) can be calculated as follows:

| | | | ||∂∂xR-∂∂xϕ ∂∂xZ|| || ∂R∂cRosϕ-∂Rc∂oϕsϕ ∂R∂cZosϕ-|| 𝒥 = ||∂y-∂y ∂y||= || ∂Rsinϕ-∂R-sinϕ ∂Rsinϕ-|| ||∂∂Rz-∂∂ϕz ∂∂Zz|| || ∂∂RZ- ∂∂ϕZ- ∂∂ZZ- || |∂R ∂ϕ ∂Z |∂R ∂ϕ ∂Z ||cosϕ − R sinϕ 0|| = ||sinϕ R cos ϕ 0||= R | 0 0 1|
If the Jacobian of a coordinate system is greater than zero, it is called a right-handed coordinate system. Otherwise it is called a left-handed system.

[next] [prev] [prev-tail] [front] [up]