[next] [prev] [prev-tail] [tail] [up]

6.8 Curl operator in general coordinates (ψ,πœƒ,ΞΆ)

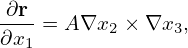
To take the curl of a vector, it should be in the covariant representation since we can make use of the fact that βˆ‡Γ—βˆ‡Ξ± = 0. Thus the curl of A is written as

βˆ‡ Γ— A = βˆ‡ Γ— (A1βˆ‡Οˆ + A2βˆ‡ πœƒ+ A3βˆ‡ ΞΆ) = βˆ‡(A1 Γ— βˆ‡ ψ+ βˆ‡A2 Γ—) βˆ‡πœƒ+ βˆ‡A3( Γ— βˆ‡ΞΆ ) ( ) βˆ‚A1- βˆ‚A1- βˆ‚A2- βˆ‚A2- βˆ‚A3- βˆ‚A3- = βˆ‚πœƒ βˆ‡ πœƒ+ βˆ‚ΞΆ βˆ‡ΞΆ Γ— βˆ‡ ψ+ βˆ‚Οˆ βˆ‡Οˆ + βˆ‚ΞΆ βˆ‡ΞΆ Γ— βˆ‡ πœƒ+ βˆ‚Οˆ βˆ‡ ψ+ βˆ‚πœƒ βˆ‡ πœƒ Γ—βˆ‡ ΞΆ 1 ( βˆ‚A2 βˆ‚A1 ) 1 (βˆ‚A1 βˆ‚A3 ) 1 ( βˆ‚A3 βˆ‚A2) = π’₯- βˆ‚-ψ-βˆ’ -βˆ‚πœƒ- π’₯ βˆ‡ ΟˆΓ— βˆ‡ πœƒ+ π’₯- -βˆ‚ΞΆ-βˆ’ -βˆ‚Οˆ- π’₯βˆ‡ ΞΆ Γ— βˆ‡ ψ + π’₯ βˆ‚πœƒ--βˆ’ βˆ‚-ΞΆ- π’₯ βˆ‡πœƒ Γ—(1βˆ‡1ΞΆ6.)
Note that taking the curl of a vector in the covariant form leaves the vector in the contravariant form.

[next] [prev] [prev-tail] [front] [up]