Deﬁnition

11.1 Deﬁnition

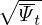
The magnetic surface average of a physical quantity G(ψ,𝜃,ϕ) is deﬁned by

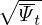∫ ∫ ∫ ( ΔΨ Gd3V ) ⟨G ⟩ ≡ ΔliΨm→0 ∫-∫ ∫--d3V-- , Δ Ψ

(222)

where the volume integration is over a small volume between two adjacent ﬂux surfaces with Ψ diﬀering by △Ψ. [This formula (with ﬁnite ΔΨ) is used in TEK code to calculate the radial heat ﬂux.]

The above 3D volume integration can also be written as a 2D surface integration. The diﬀerential volume element is given by d³V = |𝒥|dψd𝜃dϕ, where 𝒥 is the Jacobian of (ψ,𝜃,ϕ) coordinates. Using this, equation (222) is written as

( ∫ ∫ ∫ ) ⟨G⟩ = lim -∫ ∫-Δ∫Ψ-G|𝒥-|dψd𝜃dϕ Δ∫Ψ ∫→0 ΔΨ |𝒥 |dψd 𝜃dϕ ---G|𝒥|d𝜃dϕ- = ∫ ∫ |𝒥 |d𝜃dϕ , (223)

which is a 2D averaging over a magnetic surface and thus is called magnetic surface average. Note that the surface averaging of any n≠0 harmonic is zero (n is the toroidal mode number). Therefore the magnetic surface average contains only the contribution from the n = 0 component, i.e., axisymmetric component. (On the other hand, m≠0 poloidal harmonics of G can contribute to the surface average since the Jacobian has a poloidal angle dependence.) Using this and noting that 𝒥 is axisymmetric, then expression (223) is written as

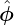∫ ⟨G⟩ = -G0(∫ψ,𝜃)|𝒥|d𝜃, |𝒥 |d𝜃

(224)

where G₀(𝜃) is deﬁned by the following Fourier expansion:

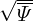+∑∞ G = Gn(ψ,𝜃)exp(− inϕ). n=−∞

(225)

_________________________________________________________________________________________________________________________

“Zonal” and “mean” components

⟨G⟩ is sometimes called the “zonal” component of G if the radial wavelength of ⟨G⟩ is much smaller than the equilibrium scale length. If the radial wavelength of ⟨G⟩ is comparable to the equilibrium scale length, ⟨G⟩ is usually called “mean” component in tokamak literature. For example, mean ﬂows are of system space scale and thus are easy to be observed in experiments. On the other hand, the “zonal” ﬂow, which usually refers to the turbulence generated secondary ﬂow, is of much smaller radial scale (the radial wavelength of zonal ﬂow is of several Larmor radius) and thus is diﬃcult to observe in experiments.

_________________________________________________________________________________________________________________________

Sometimes, we do not want the Jacobian to explicitly appear in the formula. This can be achieved by writing the diﬀerential volume element as

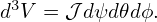d3V = Rd ϕ-dΨ-dl . |∇ Ψ| p

(226)

Using B_p = |∇Ψ|∕R, the volume element is further written as

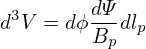dΨ d3V = dϕ---dlp Bp

(227)

Using this, the averaging deﬁned in Eq. (222) is written as

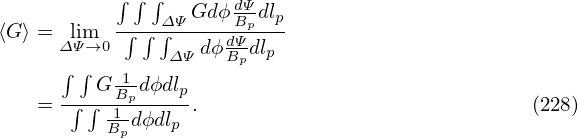
∫ ∫ ∫ dΨ ⟨G ⟩ = lim -∫-∫Δ ∫-Ψ Gd-ϕBpdlp ΔΨ→0 ΔΨ dϕdBΨpdlp ∫ ∫ G-1dϕdl = -∫-∫-Bp----p. (228) B1p dϕdlp

If G is axisymmetric, then the above equation is written as

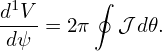∮ G-1 dlp ⟨G ⟩ =-∮-B1p---. Bpdlp

(229)

(Equation (229) is used in the GTAW code to calculate the magnetic surface averaging.) Using Eq. (168) and B_p = |∇Ψ|∕R, equation (229) can also be written as

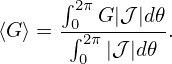∫ 2π G|𝒥|d𝜃 ⟨G ⟩ =-0∫2π------. 0 |𝒥 |d𝜃

(230)

Using the expression of the volume element dτ = |𝒥|d𝜃dϕdψ, the volume within a magnetic surface is written

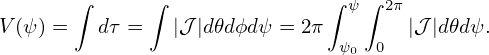∫ ∫ ∫ ψ ∫ 2π V (ψ) = dτ = |𝒥|d𝜃dϕdψ = 2π ψ 0 |𝒥 |d𝜃dψ. 0

(231)

Using this, the diﬀerential of V with respect to ψ is written as

′ dV ∫ 2π V ≡ dψ-= 2π |𝒥|d𝜃. 0

(232)

Using this, Eq. (230) is written as

⟨G⟩ =

∫ ₀^2πG|𝒥|d𝜃

[next] [front] [up]