[next] [prev] [prev-tail] [tail] [up]

8.3 Relation between Jacobian and poloidal angle πœƒ

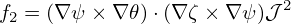
Given the definition of a magnetic surface coordinate system (ψ,πœƒ,Ο•), the Jacobian of this system is fully determined. On the other hand, given the definition of ψ, Ο•, and the Jacobian, the definition of πœƒ is fully determined (can have some trivial shifting freedoms). Next, let us discuss how to calculate πœƒ in this case. In (ψ,πœƒ,Ο•) coordinates, a line element is written

dl =-βˆ‚rdψ + βˆ‚rdπœƒ + βˆ‚rdΟ• βˆ‚Οˆ βˆ‚πœƒ βˆ‚Ο•
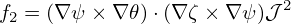(165)

The line element that lies on a magnetic surface (i.e., dψ = 0) and in a poloidal plane (i.e., dΟ• = 0) is then written

βˆ‚r dβ„“p =---dπœƒ βˆ‚ πœƒ = π’₯ βˆ‡Ο• Γ— βˆ‡ ψdπœƒ. (166)
We use the convention that dβ„“p and dπœƒ take the same sign, i.e.,
dβ„“p = |π’₯ βˆ‡Ο• Γ— βˆ‡Οˆ |dπœƒ.
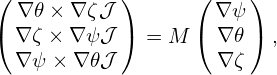(167)

Using the fact that βˆ‡Οˆ and βˆ‡Ο• are orthogonal and 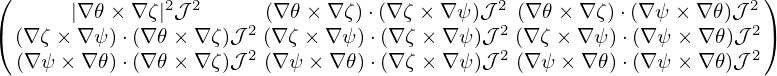βˆ‡Ο• = Λ†Ο•βˆ•R, the above equation is written as

--R--- dπœƒ = |π’₯ βˆ‡ ψ|dlp
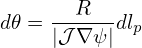(168)

Given |π’₯βˆ‡Οˆ|, Eq. (168) can be integrated to determine the πœƒ coordinate of points on a magnetic surface.

—–

- ∫ πœƒ ∫ πœƒ g π’₯ Ξ΄ = Λ†qdπœƒ = βˆ’ R2Ξ¨-β€²dπœƒ 0 0
(169)

[next] [prev] [prev-tail] [front] [up]