12.3 Relation between the partial derivatives in (ψ,𝜃,ϕ) and (ψ,𝜃,ζ) coordinates

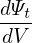
Noting the simple fact that

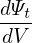(266)

where c is a constant, we conclude that

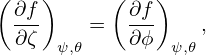(267)

(since ϕ = ζ + q(ψ)δ(ψ,𝜃), where the part q(ψ)δ(ψ,𝜃) acts as a constant when we hold ψ and 𝜃 constant), i.e., the symmetry property with respect to the new toroidal angle ζ is identical with the one with respect to the old toroidal angle ϕ. On the other hand, generally,

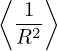(268)

and

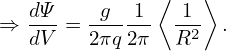(269)

In the special case that f is axisymmetric (i.e., f is independent of ϕ in (ψ,𝜃,ϕ) coordinates), then two sides of Eqs. (268) and (269) are equal to each other. Note that the partial derivatives ∂∕∂ψ and ∂∕∂𝜃 in Sec. 12.1 and 12.2 are taken in (ψ,𝜃,ϕ) coordinates. Because the quantities involved in Sec. 12.1 and 12.2 are axisymmetric, these partial derivatives are equal to their counterparts in (ψ,𝜃,ζ) coordinates.