[next] [prev] [prev-tail] [tail] [up]

12.5 Form of operator B ⋅∇ in (ψ,𝜃,ζ) coordinates

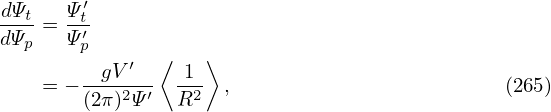
The usefulness of the contravariant form [Eq. (262] of the magnetic field lies in that it allows a simple form of B ⋅∇ operator in a coordinate system. (The operator B0 ⋅∇ is usually called magnetic differential operator.) In (ψ,𝜃,ζ) coordinate system, by using the contravariant form Eq. (262), the operator is written as

B ⋅∇f = − Ψ ′(∇ζ ×( ∇ψ )⋅∇f(ψ),𝜃,ζ)− Ψ ′q(∇ψ × ∇ 𝜃)⋅∇f(ψ,𝜃,ζ) ′ −1 ∂-- -∂- = − Ψ 𝒥 ∂𝜃 + q∂ ζ f. (270)
Next, consider the solution of the following magnetic differential equation:
B ⋅∇f = h.
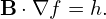(271)

where h = h(ψ,𝜃,ζ) is some known function. Using Eq. (270), the magnetic differential equation is written as

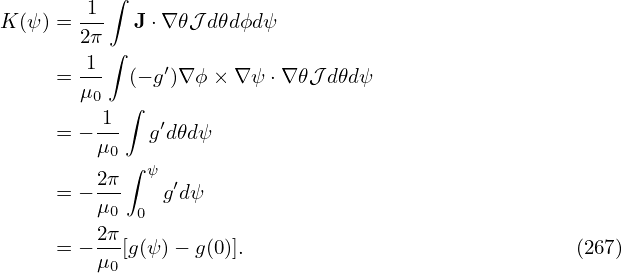( ) ∂-+ q(ψ)-∂- f = − 1-𝒥h(ψ,𝜃,ζ). ∂𝜃 ∂ζ Ψ′
(272)

Note that the coefficients before the two partial derivatives of the above equation are all independent of 𝜃 and ζ. This indicates that different Fourier harmonics in 𝜃 and ζ are decoupled. As a result of this fact, if f is Fourier expanded as

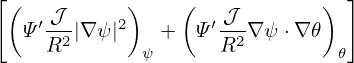∑ f(ψ,𝜃,ζ) = fmn(ψ)ei(m𝜃−nζ), m,n
(273)

(note that, following the convention adopted in tokamak literature[10], the Fourier harmonics are chosen to be ei(m𝜃−nζ), instead of ei(m𝜃+nζ)), and the right-hand side is expanded as

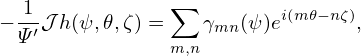1 ∑ i(m𝜃−nζ) − Ψ′𝒥 h(ψ, 𝜃,ζ) = γmn(ψ)e , m,n
(274)

then Eq. (272) can be readily solved to give

γmn fmn = i[m-−-nq].
(275)

The usefulness of the straight line magnetic coordinates (ψ,𝜃,ζ) lies in that, as mentioned previously, it makes the coefficients before the two partial derivatives both independent of 𝜃 and ζ, thus, allowing a simple solution to the magnetic differential equation.

[next] [prev] [prev-tail] [front] [up]