[next] [prev] [prev-tail] [tail] [up]

12.7 Helical angle used in tearing mode theory

Next, we discuss a special poloidal angle, which is useful in describling a perturnbation of single harmonic (m,n). This poloidal angle is defined by

n Ο‡ = πœƒβˆ’ mΞΆ,
(276)

where (m,n) are the mode numbers of the perturbation. The poloidal angle Ο‡ is often called helical angle and is special in that its definition is associated with a perturbation (the mode numbers of the perturbation appear in the definition) while the definition of the poloidal angles discussed previously only involve the equilibrium quantities.

The poloidal angle Ο‡ is designed to make 3D perturbations of the form ∼ f(ψ,mπœƒ βˆ’nΞΆ) reduce to 2D perturbations, i.e.,

βˆ‚f|| --|| = 0. βˆ‚ΞΆ ψ,Ο‡
(277)

It is ready to verify that the Jacobian of coordinates (ψ,Ο‡,ΞΆ) is equal to that of coordinates (ψ,πœƒ,ΞΆ) [proof: (π’₯β€²)βˆ’1 = βˆ‡Οˆ Γ—βˆ‡Ο‡ β‹…βˆ‡ΞΆ = βˆ‡Οˆ Γ—βˆ‡(πœƒ βˆ’ nΞΆβˆ•m) β‹…βˆ‡ΞΆ = βˆ‡Οˆ Γ—βˆ‡πœƒ β‹…βˆ‡ΞΆ = π’₯βˆ’1].

The component of B along βˆ‡Ο‡ direction (i.e., the covariant component) is written

B(Ο‡) ≑ B β‹…βˆ‡ Ο‡ β€² = βˆ’ Ξ¨ (βˆ‡ ΞΆ Γ— βˆ‡ ψ + qβˆ‡ ψ Γ— βˆ‡πœƒ)β‹…βˆ‡ (πœƒβˆ’ nΞΆβˆ•m ) = βˆ’ Ξ¨β€²(βˆ‡ ΞΆ Γ— βˆ‡ ψ β‹…βˆ‡πœƒ)+ Ξ¨ β€² n(qβˆ‡Οˆ Γ— βˆ‡ πœƒβ‹…βˆ‡ ΞΆ) n m = βˆ’ Ξ¨β€²π’₯βˆ’1 + Ξ¨β€²--qπ’₯βˆ’1 β€² βˆ’1( nq m) = Ξ¨ π’₯ m-βˆ’ 1 . (278)
At the resonant surface q = mβˆ•n, equation (278) implies B(Ο‡) = 0. The direction βˆ‡Ο‡ defines the reconnecting component of the magnetic field?

On the other hand, the component of B along βˆ‡πœƒ direction is written

(πœƒ) B ≑ B β‹…βˆ‡β€²πœƒ = βˆ’ Ξ¨ (βˆ‡ ΞΆ Γ— βˆ‡ ψ+ qβˆ‡ ΟˆΓ— βˆ‡ πœƒ)β‹…βˆ‡ πœƒ = βˆ’ Ξ¨ β€²βˆ‡ ΞΆ Γ— βˆ‡ Οˆβ‹…βˆ‡ πœƒ = βˆ’ Ξ¨ β€²π’₯ βˆ’1. (279)
Using (279) and (278), the relation between B(πœƒ) and B(Ο‡) is written as
( ) B (Ο‡) = B (πœƒ) 1 βˆ’ nq . m
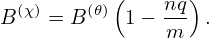(280)

[next] [prev] [prev-tail] [front] [up]