Covariant form of magnetic ﬁeld in (ψ,𝜃,ζ) coordinate system

12.8 Covariant form of magnetic ﬁeld in (ψ,𝜃,ζ) coordinate system

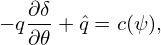
In the above, we have obtained the covariant form of the magnetic ﬁeld in (ψ,𝜃,ϕ) coordinates (i.e., Eq. (154)). Next, we derive the corresponding form in (ψ,𝜃,ζ) coordinate. In order to do this, we need to express the ∇ϕ basis vector in terms of ∇ψ, ∇𝜃, and ∇ζ basis vectors. Using the deﬁnition of the generalized toroidal angle, we obtain

g∇ ϕ = g∇ (ζ + qδ) = g∇ ζ + gq∇(δ+ gδ∇q ) = g∇ ζ + gq ∂δ-∇ψ + ∂δ-∇𝜃 + gδq′∇ ψ ∂ψ ∂𝜃 ( ∂δ ′) ∂δ = gq∂ψ-+ gδq ∇ ψ+ gq∂𝜃-∇𝜃 + g∇ ζ = g ∂(qδ)∇ ψ + gq ∂δ∇ 𝜃+ g∇ζ. (281) ∂ψ ∂𝜃

Using Eq. (281), the covariant form of the magnetic ﬁeld, Eq. (154), is written as

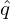( 𝒥 ∂(qδ)) ( ∂δ 𝒥 ) B = Ψ′--2∇ψ ⋅∇𝜃 + g----- ∇ ψ + gq---− Ψ′-2|∇ψ |2 ∇𝜃 + g∇ζ. R ∂ψ ∂𝜃 R

(282)

This expression can be further simpliﬁed by using equation (253) to eliminate ∂δ∕∂𝜃, which gives

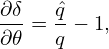
( 𝒥 ∂(qδ)) ( g2 R2 ) 𝒥 B = Ψ′--2∇ψ ⋅∇ 𝜃+ g----- ∇ ψ + − -′ − gq--− Ψ ′|∇ψ |2 -2∇ 𝜃+ g∇ ζ ( R ∂ψ ) ( Ψ 𝒥 ) R = Ψ′ 𝒥-∇ψ ⋅∇ 𝜃+ g∂(qδ) ∇ ψ + − g2 +-|∇-Ψ|2− gqR2 𝒥-∇ 𝜃+ g∇ ζ. (283) R2 ∂ψ Ψ ′ 𝒥 R2

Using B² = (|∇Ψ|² + g²)∕R², the above equation is written as

( ) ( ) B = Ψ′-𝒥-∇ψ ⋅∇ 𝜃+ g∂(qδ) ∇ ψ + − B2R2-− gqR2- 𝒥-∇ 𝜃+ g∇ ζ R2 ∂ψ Ψ ′ 𝒥 R2 ( ′ 𝒥 ∂(qδ)) ( B2 ) = Ψ R2-∇ψ ⋅∇ 𝜃+ g-∂ψ-- ∇ ψ + − Ψ′ 𝒥 − gq ∇ 𝜃+ g∇ζ. (284)

Equation (284) is the covariant form of the magnetic ﬁeld in (ψ,𝜃,ζ) coordinate system. For the particular choice of the radial coordinate ψ = −Ψ and the Jacobian 𝒥 = h(ψ)∕B² (i.e., Boozer’s Jacobian, discussed in Sec. 12.9), equation (284) reduces to

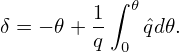( 𝒥 ∂(qδ)) B = −--2∇ψ ⋅∇ 𝜃+ g----- ∇ ψ + I(ψ )∇ 𝜃+ g(ψ)∇ ζ, R ∂ψ

(285)

with I(ψ) = h(ψ) − gq. The magnetic ﬁeld expression in Eq. (285) frequently appears in tokamak literature[28]. In this form, the coeﬃcients before both ∇𝜃 and ∇ζ depends on only the radial coordinate. In terms of I(ψ), the Jabobian can also be written as

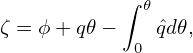𝒥 = gq+-I. B2

(286)

[next] [prev] [prev-tail] [front] [up]