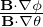[prev] [prev-tail] [tail] [up]

12.10 Radial differential operator

In solving the MHD eigenmode equations in toroidal geometry, we also need the radial differential operator ∇ψ ⋅∇. Next, we derive the form of the operator in (ψ,𝜃,ζ) coordinates. Using

∇f = 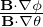∂f- ∂ψ∇ψ + 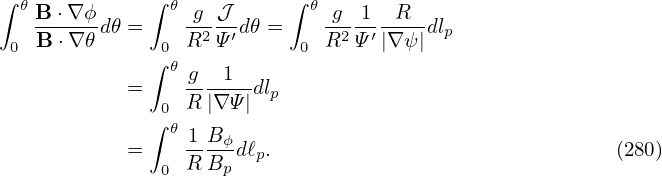∂f- ∂ 𝜃∇𝜃 + 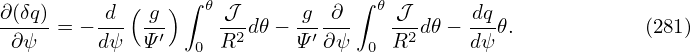∂f- ∂ζ∇ζ,

the radial differential operator is written as

∇ ψ ⋅∇f = |∇ ψ|2∂f-+ (∇𝜃 ⋅∇ ψ)∂f-+ (∇ζ ⋅∇ψ )∂f- ∂ψ ∂ 𝜃 ∂ζ 2∂f- ∂f- ∂f- = |∇ ψ| ∂ψ + (∇𝜃 ⋅∇ ψ)∂ 𝜃 + {∇ [ϕ − qδ(ψ,𝜃)]⋅∇ ψ}∂ζ 2∂f ∂f ∂f = |∇ ψ| ∂ψ-+ (∇𝜃 ⋅∇ ψ)∂-𝜃 − ∇ [qδ]⋅∇ ψ∂ζ ∂f ∂f ∂f = |∇ ψ|2---+ (∇𝜃 ⋅∇ ψ)---− [q∇δ +δ∇q ]⋅∇ψ --- ∂ψ ∂ 𝜃 [ ( ∂ζ) ] = |∇ ψ|2∂f-+ (∇𝜃 ⋅∇ ψ)∂f-− q ∂δ-∇ψ + ∂δ∇ 𝜃 + δq′∇ ψ ⋅∇ ψ∂f- ∂ψ ∂ 𝜃 [ ∂ψ ∂𝜃 ] ∂ζ 2∂f- ∂f- ∂-(qδ) 2 ∂δ- ∂f- = |∇ ψ| ∂ψ + (∇𝜃 ⋅∇ ψ)∂ 𝜃 − ∂ ψ |∇ψ| + q∂𝜃 ∇𝜃 ⋅∇ψ ∂ζ, (290)
where ∂(qδ)∕∂ψ and q∂δ∕∂𝜃 are given respectively by Eqs. (259) and (253). Using the above formula, ∇ψ ⋅∇ζ is written as
[ ] ∂(qδ) 2 ∂δ- ∇ ψ ⋅∇ζ = − ∂ψ |∇ ψ| + q∂𝜃∇ 𝜃⋅∇ ψ .
(291)

This formula is used in GTAW code.

[prev] [prev-tail] [front] [up]