[next] [prev] [prev-tail] [tail] [up]

12.9 Form of operator (B ×∇ψ∕B2) ⋅∇ in (ψ,𝜃,ζ) coordinates

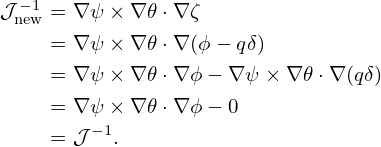
In solving the MHD eigenmode equations in toroidal geometries, besides the B ⋅∇ operator, we will also encounter another surface operator (B×∇ψ∕B2) ⋅∇. Next, we derive the form of the this operator in (ψ,𝜃,ζ) coordinate system. Using the covariant form of the equilibrium magnetic field [Eq.  (284)], we obtain

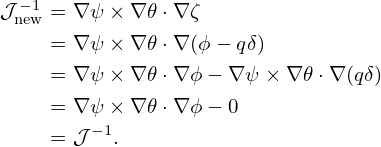( ) B-×-∇-ψ = -1- − B2-𝒥 − gq ∇ 𝜃× ∇ ψ+ -g-∇ ζ × ∇ ψ. B2 B2 Ψ ′ B2
(287)

Using this, the (B ×∇ψ∕B2) ⋅∇ operator is written as

( ) B-×-∇-ψ -1- B2- − 1 ∂- -g- −1 ∂- B2 ⋅∇ = B2 Ψ′ 𝒥 + gq 𝒥 ∂ζ + B2 𝒥 ∂𝜃 (288) ( 1 𝒥 −1 ) ∂ 𝒥−1 ∂ = --′ + g-2-q ---+g --2---, (289) Ψ B ∂ζ B ∂𝜃
which is the form of the operator in (ψ,𝜃,ζ) coordinate system.

Examining Eq. (289), we find that the coefficients before the two partial derivatives will be independent of 𝜃 and ζ if the Jacobian 𝒥 is chosen to be of the form 𝒥 = h(ψ)∕B2, where h is some magnetic surface function. It is obvious that the independence of the coefficients on 𝜃 and ζ will be advantageous to some applications. The coordinate system (ψ,𝜃,ζ) with the particular choice of 𝒥 = h(ψ)∕B2 is called the Boozer coordinates. The usefulness of the new toroidal angle ζ is highlighted in Boozer’s choice of the Jacobian, which makes both B ⋅∇ and (B ×∇ψ∕B2) ⋅∇ be a constant-coefficient differential operator. For other choices of the Jacobian, only the B⋅∇ operator is a constant-coefficient differential operator.

[next] [prev] [prev-tail] [front] [up]