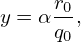Numerical veriﬁcation of the ﬁeld-aligned coordinates

13.7 Numerical veriﬁcation of the ﬁeld-aligned coordinates

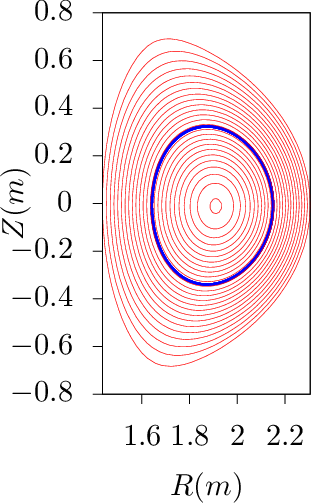
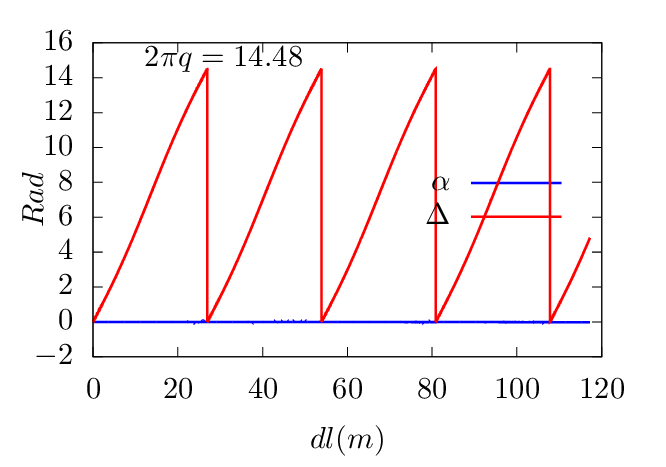
The generalized toroidal angle α is numerically calculated in my code. To verify B ⋅∇α = 0 along a magnetic ﬁeld-line, ﬁgure 26 plots the values of α along a magnetic ﬁeld line, which indicates that α is constant. This indicates the numerical implementation of the ﬁeld-aligned coordinates is correct.

pict pict

Fig. 26: Left: Projection of a ﬁeld line on the poloidal plane. Right: the value of Δ and α along the magnetic ﬁeld line. Here α is deﬁned by α = ϕ−Δ, where ϕ is the usual cylindrical toroidal angle and Δ = ∫ ₀^𝜃 B⋅∇-ϕ
B⋅∇ 𝜃

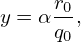d𝜃.

Binormal wavenumber

Let us introduce the binormal wavenumber, which is frequently used in presenting turbulence simulation results. Deﬁne the binormal direction s by

s =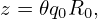

which is a unit vector lying on a magnetic surface and perpendicular to B. The binormal wavenumber of a mode is deﬁned by

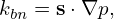kbn = s⋅∇p,

(339)

where p is the phase of the mode. Consider a mode given by exp(ik_ψψ + im𝜃 − inζ), then the phase p = k_ψψ + m𝜃 − nζ. Then k_bn is written as

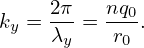
kbn = B-×-∇-Ψ-⋅∇ (kψ ψ+ m 𝜃− nζ) |B × ∇ Ψ| B-×-∇-Ψ- = |B × ∇ Ψ| ⋅∇ (m 𝜃 − n ζ), (340)

where the radial phase k_ψψ does not appear since B ×∇Ψ ⋅∇ψ = 0. The above expression can be further written as

kbn =----1--- [mB × ∇Ψ ⋅∇ 𝜃− nB × ∇Ψ ⋅∇ ζ] |B × ∇Ψ | ----1--- = |B × ∇Ψ |[mB ⋅∇Ψ × ∇ 𝜃− nB ⋅∇Ψ × ∇ ζ] nB⋅ [m ] = |B-×-∇Ψ-| n-∇Ψ × ∇ 𝜃− ∇ Ψ × ∇ ζ . (341)

Equation (341) is the general expression of the binormal wavenumber. On the resonant surface of the mode, i.e., q(ψ) = m∕n, then the above expression is written as

nB ⋅ kbn = |B-×∇-Ψ|[q∇Ψ × ∇𝜃 − ∇Ψ × ∇ ζ].

(342)

Using Eq. (262), i.e., B = −(∇ζ ×∇Ψ + q∇Ψ ×∇𝜃), the above expression is written as

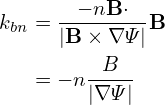
− nB⋅ kbn = |B-×-∇-Ψ|B = − n-B--- |∇Ψ |

Using B_p = |∇Ψ|∕R, the above equation is written

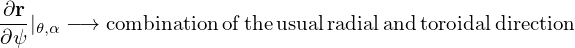kbn = − n-B-- RBp

(343)

which indicates the binormal wavenumber generally depends on the poloidal angle. For large aspect-ratio tokamak, we have B_ϕ ≈ B, q ≈ B_ϕr∕(B_pR). Then Eq. (343) is written

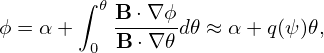nq kbn ≈ − --, r

(344)

which indicates the binormal wavenumber are approximately independent of the poloidal angle. Since m = nq on a resonant surface, the above equation is written |k_bn|≈ m∕r, which is the usual poloidal wave number. Due to this relation, the binormal wavenumber k_bn is often called the poloidal wavenumber and denoted by k_𝜃 in papers on tokamak turbulence. In the GENE code, y coordinate is deﬁned by y = αr₀∕q₀. Then the k_y of a mode of toroidal mode number n is given by k_y = 2π∕λ_y where λ_y = λ_αr₀∕q₀ and λ_α = 2π∕n. Then k_y is written as k_y = nq₀∕r₀, which is similar to the binormal deﬁned above. For this reason, k_y of GENE code is also called binormal wave-vector, which is in fact not reasonable because neither ∂r∕∂y or ∇y is along the binormal direction.

[prev] [prev-tail] [front] [up]