Is the above B divergence-free?

14.1 Is the above B divergence-free?

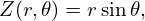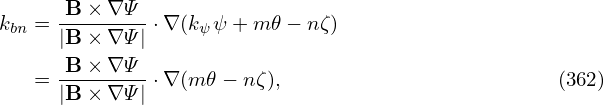
Since the above ﬁeld is derived from the general form given by Eq. (10), it is guaranteed that the ﬁeld is divergence-free. In case of any doubt, let us directly verify this. Write B as

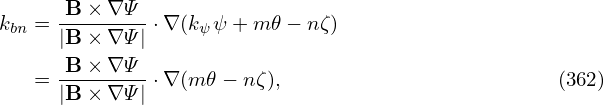B = B (1)𝒥∇ 𝜃× ∇ ϕ+ B (2)𝒥∇ ϕ× ∇r + B (3)𝒥∇r × ∇ 𝜃,

(359)

where 𝒥 is the Jacobian of (r,𝜃,ϕ) coordinates; B⁽¹⁾, B⁽²⁾, and B⁽³⁾ are given by

B(1) = B ⋅∇r

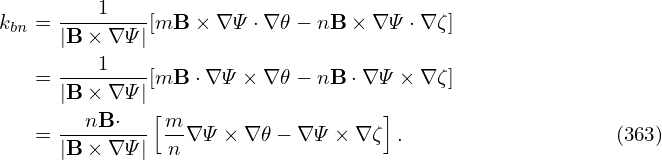(360)

B(2) = B ⋅∇𝜃

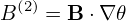(361)

B(3) = B ⋅∇ϕ

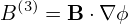(362)

Use B_p given by (356), then B⁽¹⁾, B⁽²⁾, and B⁽³⁾ are written as

(1) B = 0,

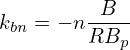(363)

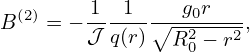B (2) = − 1-1--∘--g0r--, 𝒥 q(r) R20 − r2

(364)

and

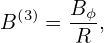B(3) = B-ϕ, R

(365)

respectively. Then, by using the divergence formula in (r,𝜃,ϕ) coordinates, ∇⋅ B is written as

( (1) (2) (3) ) ∇ ⋅B = 1- ∂B---𝒥-+ ∂B---𝒥-+ ∂B---𝒥- 𝒥 ∂r ∂𝜃 ∂ϕ 1 ( ∂B (2)𝒥 ) = 𝒥- 0+ --∂𝜃---+ 0 ( ) = 1--∂- − -1--∘--g0r---- 𝒥 ∂𝜃 q(r) R20 − r2 = 0 (366)

i.e., B in this case is indeed divergence-free.

[next] [front] [up]