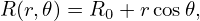
Assume magnetic surfaces of a magnetic configuration are known and given by
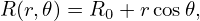 | (345) |
 | (346) |
where (r,𝜃) are two parameters and r is magnetic surface label (i.e., ∂Ψ∕∂𝜃|r = 0). The above parametric equations specify a series of concentric-circular magnetic surfaces.
Assume the toroidal field function g(r) = RBϕ is given. Then the toroidal magnetic field is determined by Bϕ = g∕R. Further assume the safety factor profile q(r) is given, then the magnetic field is fully determined. Next, let us derive the explicit form of the poloidal magnetic field Bp, which is given by
 | (347) |
which involves the poloidal magnetic flux Ψp. Therefore our task is to express Ψp in terms of q and g. Using q(r) = dΨt∕dΨp, we obtain
dΨp =  dΨt, dΨt,
|
Integrate the above equation over r, we obtain
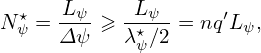 | (348) |
which an be written as
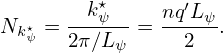 | (349) |
where use has been made of Ψt = ∫ 0r ∫ −ππBϕrdrd𝜃. Using Bϕ = g∕R and R = R0 + r cos𝜃, the above equation is written
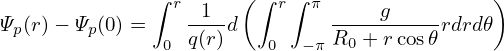 | (350) |
Using maxima (an open-source computer algebra system), the above integration over 𝜃 can be performed analytically, giving
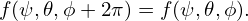 | (351) |
Using this, equation (350) is written as
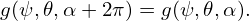 | (352) |
which can be simplified as
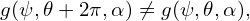 | (353) |
This is what we want—the expression of the poloidal magnetic flux in terms of q and g. [Another way of obtaining Eq. (353) is to use Eq. (160), i.e.,
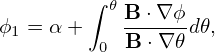 | (354) |
where 𝒥 is the Jacobian of the (r,𝜃,ϕ) coordinates and is given by 𝒥 = R(R𝜃Zr −RrZ𝜃) = −Rr. Then Eq. (354) is simplified as
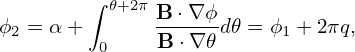 | (355) |
which, after being integrated over r, gives Eq. (353).]
Using Eq. (353), the poloidal magnetic field in Eq. (347) is written as
[Using the formulas ∇r = −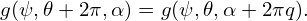 (Z𝜃
(Z𝜃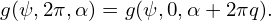 −R𝜃
−R𝜃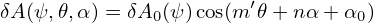 ) and 𝒥 = R(R𝜃Zr −RrZ𝜃), where 𝒥 is the Jacobian of the
(r,𝜃,ϕ) coordinates, we obtain 𝒥 = −Rr and ∇r = cos𝜃
) and 𝒥 = R(R𝜃Zr −RrZ𝜃), where 𝒥 is the Jacobian of the
(r,𝜃,ϕ) coordinates, we obtain 𝒥 = −Rr and ∇r = cos𝜃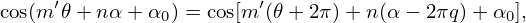 + sin𝜃
+ sin𝜃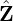 , ∇ϕ =
, ∇ϕ = 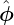 ∕R. Then Eq. (356) is
written as
∕R. Then Eq. (356) is
written as
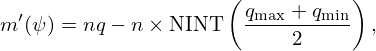 | (357) |
This is the explicit form of the poloidal magnetic field in terms of g and q. The magnitude of Bp is written as
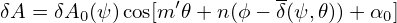 | (358) |
Note that both Bp and Bϕ depend on the poloidal angle 𝜃.]
I use Eq. (353) to compute the 2D data of Ψ (Ψ = Ψp∕2π) on the poloidal plane when creating a numerical G-eqdsk file for the above magnetic configuration (Fortran code is at /home/yj/project_new/circular_configuration_with_q_given).
Assume that the poloidal plasma current is zero, then g(r) = RBϕ is a constant independent of r. This is always assumed by the authors who use concentric-circular configuration but is seldom explicitly mentioned.
In analytical work, 1∕R dependence on (r,𝜃) is often approximated as
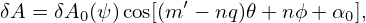 = = 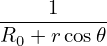 = = 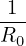 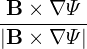 ≈ ≈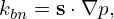 (1 − 𝜀cos𝜃), (1 − 𝜀cos𝜃),
|
where 𝜀 = r∕R0 is the local inverse aspect ratio.