14.5 Safety factor profile

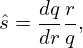
The magnetic shear for a concentric-circular configuration is defined by

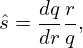(385)

where r is the minor radius of a magnetic surface. The above expression can be re-arranged as

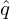(386)

Integrating the above equation over r and assuming ŝ is a constant, we obtain

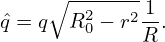(387)

Performing the integration, the above equation is written as

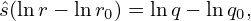(388)

where q₀ = q(r₀). Equation (388) can be finally written as

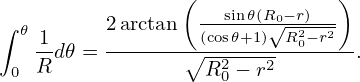(389)

This is a profile with a constant magnetic shear s. In Ben’s toroidal ITG simulation, the following q profile is used:

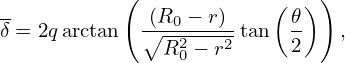(390)

with q′(r₀) = ŝq₀∕r₀. This is a linear profile over r, with the values of q and the shear at r = r₀ being q₀ and ŝ, respectively.