16.2 Normalized internal inductance

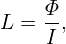
The self-inductance of a current loop is defined as the ratio of the magnetic flux Φ traversing the loop and its current I:

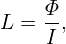(477)

where

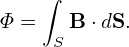(478)

It can be proved that L is independent of the current I in the loop, i.e., L is fully determined by the shape of the loop.

On the other hand, the energy contained in the magnetic field produced by the loop current is given by

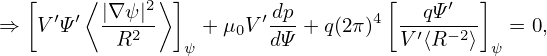(479)

where the volume includes all space where B is not negligible. It can be proved that (to be proved) W, L, and I are related to each other by:

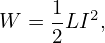(480)

i.e.,

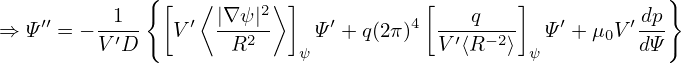(481)

which can be considered an equivalent definition of the self-inductance.

The internal inductance L_i of tokamak plasma is defined in such a way that W only includes the magnetic energy within the plasma. Specifically, L_i is defined by

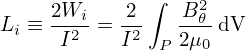(482)

where the integration over the plasma volume P and only the poloidal field B_𝜃 appears in the integration since plasma current produces only the poloidal magnetic field.

The normalized internal inductance l_i is defined as

(483)

where R₀ is the major radius of the device (equal to R of the magnetic axis). Using Eq. (482), expression (483) is written as

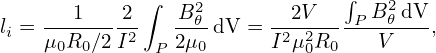(484)

which is the definition of l_i used in the ITER design.

Another way of defining the normalized internal inductance is

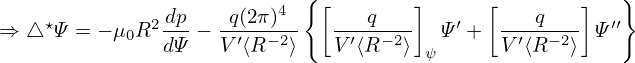(485)

where ⟨…⟩_S is the surface average over the plasma boundary. For circular cross section with minor radius a and assuming B_𝜃 is independent of the poloidal angle, then, Ampere’s law gives B_𝜃(a) = μ₀I∕(2πa). Then ⟨B_𝜃²⟩_S is approximated as

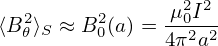(486)

Using this and V ≈ πa²2πR₀,  Eq. (485) is written as

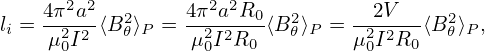(487)

which agrees with the definition in Eq. (484).

The normalized internal inductance reflects the peakness of the current density profile in the toroidal plasma: a small value of l_i corresponds to a broad current profile.