16.3 Cylindrical tokamak

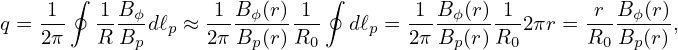
For a large aspect-ratio, circular cross section tokamak, the R on a magnetic surface is nearly constant, R ≈ R₀. The poloidal angle dependence of the magnetic field can be neglected, i.e., B_ϕ(r,𝜃) ≈ B_ϕ(r), and B_p(r,𝜃) ≈ B_p(r), where r is the minor radius of the relavent magnetic surface. Using these, the safety factor in Eq.  (37) is approximated to

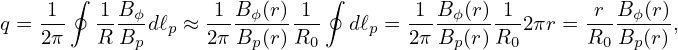(488)