[next] [prev] [prev-tail] [tail] [up]

16.4 Coils system of EAST tokamak

Poloidal field (PF) coils

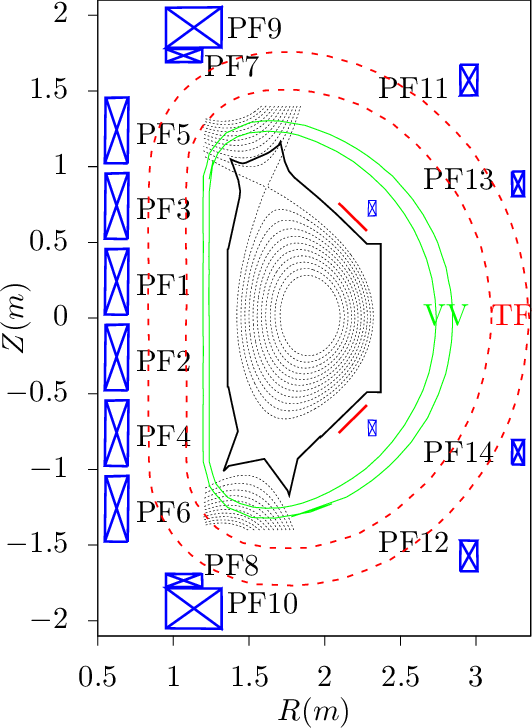
EAST has 12 independently powered superconducting poloidal field (PF) coils, as is shown in Fig. 33.

pict

Fig. 33: Coils system of EAST tokamak. Coils PF1 to PF6 are Central Solenoide (CS) coils with 120 turns/coil. Both PF11 and PF12 have 64 turns, Both PF13 and PF14 have 32 turns. PF7 and PF9 are adjacent to each other and connected in series and thus are considered as one independent coil, with total turns being 248. Similarly PF8 and PF10 are connected in series with total 248 turns. All the PF coils can be considered as shaping coils since they all have effects in shaping the plasmas. In practice, they are further classified according to their main roles. PF1 to PF6 form a solenoid in the center of the torus and thus called Central Solenoide (CS) coils. Their main role is to induce electric field to drive current in the plasma and heat the plasma. As a result, they are often called “Ohm heating coils”. PF13 and PF14 are mainly used to control (slow) vertical plasma displacement and thus are often called “vertical field coils” or “position control coils”. PF11 and PF12 are used to triangularize the plasma and thus is called “shaping coils”. PF7+PF9 and PF8+PF10 are often called (by EAST operators) as “big coils” or “divertor coils” since they have the largest number of turns and current and are used to elongate/shape the plasma to diverter configurations. IC1 and IC2 are copper coils (2turn/coil), which are connected in anti-series and thus have opposite currents. They are close to the plasma (just behind the first wall and within the vacuum vessel) and are used to control fast plasma displacements, specifically VDEs (vertical displacement events). IC1 and IC2 are often called “fast control coils”. Maximum current per turn in PF coils is 14.5kA. Locations of PF coils are from Refs. [24][9]. The inner green D-shaped structure corresponds to the vaccum vessel wall and the outer red dashed D-shape corresponds to the TF-coils. Note that PF1-14 coils are all located outside of the TF-coils. The small blue circles are “flux loops” measuring the poloidal magnetic flux. Red coils are RMP copper coils.
Toroidal magnetic Field (TF) coils and toroidal magnetic field of EAST tokamak

Using Ampere’s circuital law

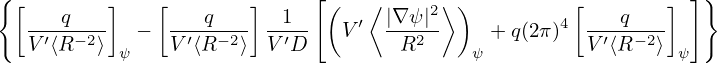∮ B ⋅dl = μ0I,
(489)

along the toroidal direction and assuming perfect toroidal symmetry, we obtain

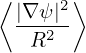2πRB ϕ = μ0I,
(490)

which gives

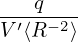Bϕ = -μ0I = 2× 10−7 I-. 2πR R
(491)

Neglecting the poloidal current contributed by the plasma, the poloidal current is determined solely by the current in the TF coils. The EAST tokamak has 16 groups of TF coils with 132turns/coil (I got to know the number of turns from ZhaoLiang Wang: φ × R = 12 × 11 = 132). Denote the current in a single turn by Is, then Eq. (491) is written

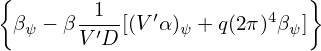μ0 × 16× 132 × Is −4Is Bϕ = ------2πR-------= 4.224 × 10 R-
(492)

Using this formula, the strength of the toroidal magnetic field at R = 1.8m for Is = 104A is calculated to be Bϕ = 2.34T. This was one of the two scenarios often used in EAST experiments (another scenario is Is = 8 × 103A). (The limit of the current in a single turn of the TF coils is 14.5kA (from B. J. Xiao’s paper [29]).

Note that the exact equilibrium toroidal magnetic field Bϕ is given by Bϕ = g(Ψ)∕R. Compare this with Eq. (491), we know that the approximation made to obtain Eq. (492) is equivalent to g(Ψ) ≈ μ0ITF∕2π, i.e. assuming g is a constant. The poloidal plasma current density jpol is related to g by jpol = g′(Ψ)Bp∕μ0. The constant g corresponds to zero plasma poloidal current, which is consistent to the assumption used to obtain Eq. (492).

Let us estimate the safety factor value near the plasma edge using the total plasma current and the current in a single turn of TF coils Is. For divertor magnetic configuration, the plasma edge is at the saperatrix, where q →∞. To get a characteristic safety factor value that is finite, one often chooses the edge to be the magnetic surface that encloses 95% of the poloidal magnetic flux. Denote this surface by S95 and the value of q at this surface by q95, which is given by

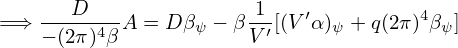q95 ≈ Bϕ,axis-a--, Bp Raxis
(493)

where a is the minor radius of the surface S95, and Raxis the major radius of the magnetic axis, Bϕ,axis is the the magnitude of toroidal magnetic field at the magnetic axis, and Bp is the average poloidal magnetic field on the surface, Bp ≈ μ0Ip∕(2πa). Using Eq. (492), Eq. (493) is written as

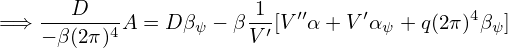4.224×-10−4Is2πa2- q95 ≈ μ0Ip R2axis,
(494)

For EAST, tipically Raxis = 1.85m and a = 0.45m. Using this, we obtain

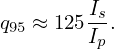Is q95 ≈ 125Ip.
(495)

RMP coils of EAST

The so-called resonant magnetic perturbation (RMP) coils are 3D coils that are used to suppress or mitigate edge localized modes. The shape and location of RMP coils of EAST tokamak are plotted in Fig. 34.

 

pict pict

Fig. 34: Location of the RMP coils on EAST tokamak in 3D view (left) and poloidal view (right).

 

[next] [prev] [prev-tail] [front] [up]