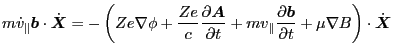Doting Eq. (21) with
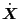 , we obtain
, we obtain
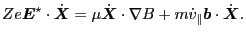 |
(28) |
Using
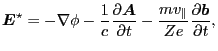 |
(29) |
Eq. (28) is written as
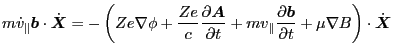 |
(30) |
Using Eq. (7), i.e.,
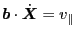 , the above equation is written as
, the above equation is written as
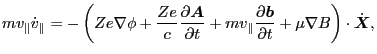 |
(31) |
which gives the time change rate of the parallel velocity
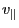 . By
using
. By
using
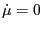 and
and 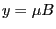 , the time change rate of the
perpendicular velocity is written as
, the time change rate of the
perpendicular velocity is written as
Next, calculate the total time derivative of the particle energy. The particle
energy
 is the sum of the kinetic and potential energy, i.e.,
is the sum of the kinetic and potential energy, i.e.,
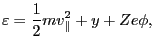 |
(33) |
from which we obtain
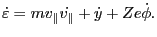 |
(34) |
Using Eqs. (31) and (32), the right-hand side of Eq.
(34) is written as
For the equilibrium case, electromagnetic field is independent of time, so the
result of the above expression is zero, indicating that energy is a constant
of the motion.
YouJun Hu
2014-05-19
![]() , we obtain
, we obtain