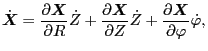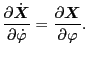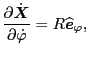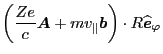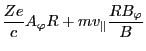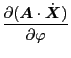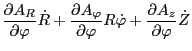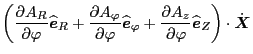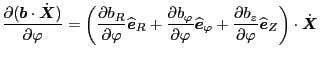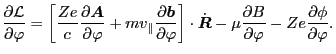Next, we work in cylindrical coordinates
 and prove that the
generalized momentum conjugating to the toroidal angle
and prove that the
generalized momentum conjugating to the toroidal angle  is a constant
of motion for axisymmetric electromagnetic field. The generalized momentum
conjugating to
is a constant
of motion for axisymmetric electromagnetic field. The generalized momentum
conjugating to 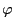 is defined by
is defined by
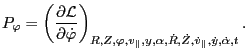 |
(36) |
Using the Lagrangian given in Eq. (1), Eq. (36) is
written as
Noting that
 , we obtain
, we obtain
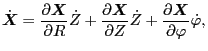 |
(38) |
from which we get
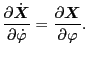 |
(39) |
Further we note that
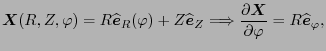 |
(40) |
where
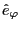 is the toroidal unit vector. Thus we obtain that
is the toroidal unit vector. Thus we obtain that
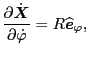 |
(41) |
Using this, Eq. (37) is written as
Define
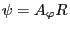 , then the above equation is written as
, then the above equation is written as
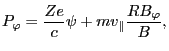 |
(42) |
which agrees with Eq. (17) in Porcelli's paper[1]. Next we
calculate the total time derivative of
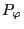 , which is given by the
Euler-Lagrangian equation corresponding to
, which is given by the
Euler-Lagrangian equation corresponding to 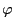 ,
,
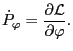 |
(43) |
In order to calculate the partial derivative of
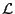 with respect to
with respect to
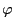 , we write
, we write
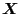 in terms of the cylindrical coordinate,
in terms of the cylindrical coordinate,
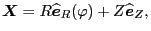 |
(44) |
the time derivative of which is
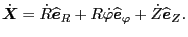 |
(45) |
(Note that
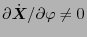 .) Then we
have
.) Then we
have
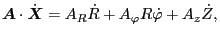 |
(46) |
from which we obtain
Similarly, we obtain
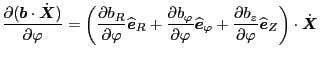 |
(48) |
Using these, the partial derivative of
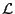 with respect to
with respect to 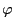 can be calculated as
can be calculated as
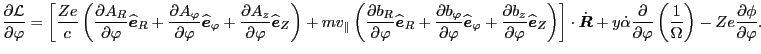 |
(49) |
The second last term on the right-hand side of Eq. (49) can be
further calculated as
Using 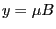 and
and
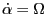 in the above equation, we obtain
in the above equation, we obtain
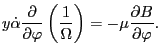 |
(51) |
Using Eq. (51) in Eq. (49) yields
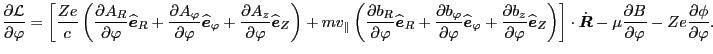 |
(52) |
For toroidal symmetrical equilibrium, the partial derivatives with respect to
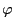 are all zeros. In this case Eq. (52) reduces to
are all zeros. In this case Eq. (52) reduces to
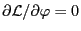 . Using the Euler-Lagrange equation, we
obtain
. Using the Euler-Lagrange equation, we
obtain
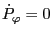 , i.e.,
, i.e.,
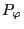 is a constant of the
motion in symmetrical field. [Note in passing that Eq. (52) is
different from Eq. (32) in Porcelli's paper[1], which is
given by
is a constant of the
motion in symmetrical field. [Note in passing that Eq. (52) is
different from Eq. (32) in Porcelli's paper[1], which is
given by
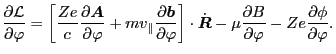 |
(53) |
Porcelli's equation is obviously wrong since it can not recover the correct
result
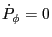 for axisymmetrical electromagnetic field.]
for axisymmetrical electromagnetic field.]
YouJun Hu
2014-05-19
![]() and prove that the
generalized momentum conjugating to the toroidal angle
and prove that the
generalized momentum conjugating to the toroidal angle ![]() is a constant
of motion for axisymmetric electromagnetic field. The generalized momentum
conjugating to
is a constant
of motion for axisymmetric electromagnetic field. The generalized momentum
conjugating to ![]() is defined by
is defined by