The time change rate of
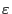 and
and
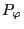 is given respectively
by Eqs. (35) and (52), i.e.,
is given respectively
by Eqs. (35) and (52), i.e.,
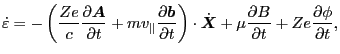 |
(54) |
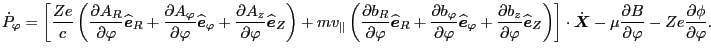 |
(55) |
From Eqs. (54) and (55), we know that the energy
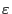 is conserved for motion in time independent field while
is conserved for motion in time independent field while
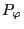 is conserved for motion in toroidal symmetrical field. For the
motion in a toroidal symmetrical equilibrium field superposed by a coherent
perturbation
is conserved for motion in toroidal symmetrical field. For the
motion in a toroidal symmetrical equilibrium field superposed by a coherent
perturbation
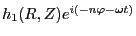 with
with
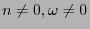 , neither of
, neither of
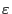 and
and
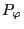 is conserved. In
this case we can construct a new conservative quantity by combining
is conserved. In
this case we can construct a new conservative quantity by combining
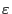 and
and
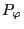 . Define
. Define
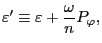 |
(56) |
then it is easy to verify that
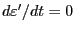 when including only
the contribution of the perturbation up to the order
when including only
the contribution of the perturbation up to the order
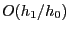 .
.
YouJun Hu
2014-05-19
![]() and
and
![]() is given respectively
by Eqs. (35) and (52), i.e.,
is given respectively
by Eqs. (35) and (52), i.e.,