Next, we derive the guiding center drift. Using equation (13), we
obtain
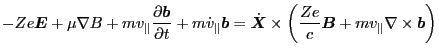 |
(57) |
Taking cross product of the above equation with
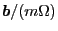 ,
we obtain
,
we obtain
![$\displaystyle \frac{1}{m \Omega} \ensuremath{\boldsymbol{b}} \times \left( - Z ...
...B}} + m v_{\parallel} \nabla \times \ensuremath{\boldsymbol{b}} \right) \right]$](img120.png) |
(58) |
The right-hand side of the above equation is simplified as
Using this, Eq. (58) is written as
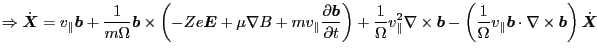 |
(60) |
![$\displaystyle \Rightarrow \dot{\ensuremath{\boldsymbol{X}}} = v_{\parallel} \en...
...s \ensuremath{\boldsymbol{b}} \right) \dot{\ensuremath{\boldsymbol{X}}} \right]$](img126.png) |
(61) |
Equation (61) contains
 drift
and
drift
and 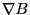 drift. Next we examine the terms in the square bracket of Eq.
(61), which can be further written as
drift. Next we examine the terms in the square bracket of Eq.
(61), which can be further written as
Using this, Eq. (61) is written as
![$\displaystyle \Rightarrow \dot{\ensuremath{\boldsymbol{X}}} = v_{\parallel} \en...
...l{b}} \right) \times \dot{\ensuremath{\boldsymbol{X}}}_{\perp} \right] \right\}$](img135.png) |
(62) |
Besides
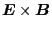 drift,
drift, 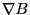 drift, and
magnetic curvature drift, Eq. (62) also contains additional terms
(the terms in the square bracket). The first term in the square bracket is
usually small compared with other terms, so this term is usually ignored (this
term appears in equation (181) of Boozer's paper[2], and is
said to be ignorably small in his paper). We now exxamine the last term, i.e.,
drift, and
magnetic curvature drift, Eq. (62) also contains additional terms
(the terms in the square bracket). The first term in the square bracket is
usually small compared with other terms, so this term is usually ignored (this
term appears in equation (181) of Boozer's paper[2], and is
said to be ignorably small in his paper). We now exxamine the last term, i.e.,
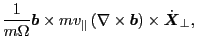 |
(63) |
which can be written as
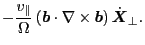 |
(64) |
In Eq. (66) of Ref. [3], it is pointed out that
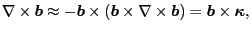 |
(65) |
which is correct in the order considered here (I do not check this). This
indicates that
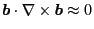 .
Using this, we know the expression in Eq. (64) is approximately
zero. Thus the terms in the square bracket of Eq. (62) can be
dropped. Then Eq. (62) reduces to
.
Using this, we know the expression in Eq. (64) is approximately
zero. Thus the terms in the square bracket of Eq. (62) can be
dropped. Then Eq. (62) reduces to
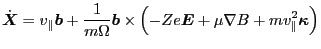 |
(66) |
YouJun Hu
2014-05-19
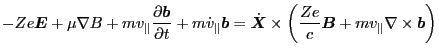
![$\displaystyle - \frac{1}{m \Omega} \left( \ensuremath{\boldsymbol{b}} \cdot \do...
...s \ensuremath{\boldsymbol{b}}
\right) \right] \dot{\ensuremath{\boldsymbol{X}}}$](img121.png)
![$\displaystyle = - v_{\parallel} \left( \ensuremath{\boldsymbol{b}} + \frac{v_{\...
...la \times \ensuremath{\boldsymbol{b}} \right]
\dot{\ensuremath{\boldsymbol{X}}}$](img122.png)
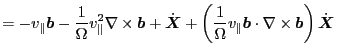
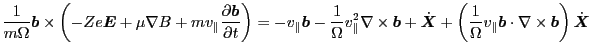
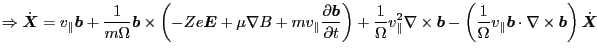
![$\displaystyle \frac{1}{m \Omega} \left[ \ensuremath{\boldsymbol{b}} \times m v_...
...s
\ensuremath{\boldsymbol{b}} \right) \dot{\ensuremath{\boldsymbol{X}}} \right]$](img129.png)
![$\displaystyle = \frac{1}{m \Omega} \left\{ \ensuremath{\boldsymbol{b}} \times m...
...math{\boldsymbol{b}} \right) \dot{\ensuremath{\boldsymbol{X}}}
\right] \right\}$](img130.png)
![$\displaystyle = \frac{1}{m \Omega} \left\{ \ensuremath{\boldsymbol{b}} \times m...
...oldsymbol{b}} \right) \times
\dot{\ensuremath{\boldsymbol{X}}} \right] \right\}$](img131.png)
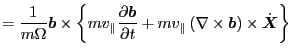
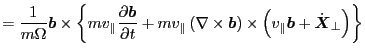
![$\displaystyle = \frac{1}{m \Omega} \ensuremath{\boldsymbol{b}} \times \left\{ m...
...l{b}} \right) \times
\dot{\ensuremath{\boldsymbol{X}}}_{\perp} \right] \right\}$](img134.png)