The time evolution of
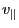 is given by Eq. (27), i.e.,
is given by Eq. (27), i.e.,
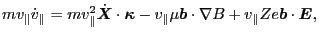 |
(74) |
which involves the term
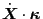 . Next we
try to simplify this term. Using Eq. (71), the term is written as
. Next we
try to simplify this term. Using Eq. (71), the term is written as
Using this in Eq. (74) gives
which can be arranged as
which, after some straightforward algebras, can be arranged into the following
forms
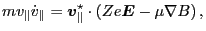 |
(75) |
which agrees with Eq. (15) in Todo's paper[4].
YouJun Hu
2014-05-19
![]() is given by Eq. (27), i.e.,
is given by Eq. (27), i.e.,
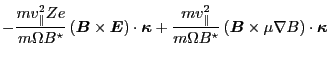
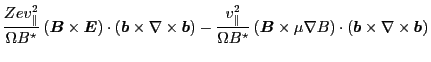
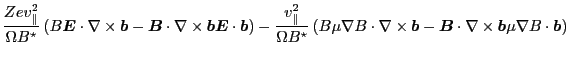
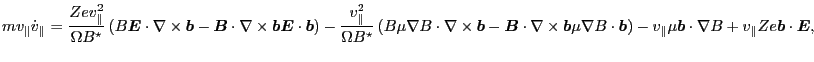
![$\displaystyle m v_{\parallel} \dot{v}_{\parallel} = \left[ \frac{v_{\parallel}^...
...l{b}} +
v_{\parallel} \ensuremath{\boldsymbol{b}} \right] \cdot \mu \nabla B, $](img159.png)