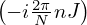[prev] [prev-tail] [tail] [up]

4.4 Proof of the inverse DFT

In order to solve the linear algebraic equations (34) for hj, multiply both sides of each equation by exp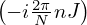( 2π- ) − iN nJ, where J is an integer between [0,N − 1], and then add all the equations together, which yields

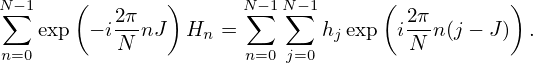N∑ −1 ( ) N∑−1N∑− 1 ( ) exp − i2πnJ Hn = hjexp i2π-n(j − J) . n=0 N n=0j=0 N
(47)

Interchanging the sequence of the two summation on the right-hand side, equation (47) is written

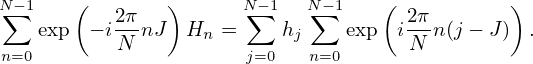N∑ −1 ( 2π ) N∑−1 N∑−1 ( 2π ) exp − iN-nJ Hn = hj exp iN-n(j − J) . n=0 j=0 n=0
(48)

Using the fact that (verified by Wolfram Mathematica)

N∑−1 [ 2π ] exp iN--n(j − J) = N δjJ, n=0
(49)

where δjJ is the Kroneker Delta, equation (48) is written

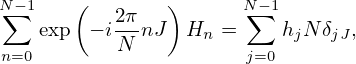N −1 ( ) N−1 ∑ exp − i2πnJ Hn = ∑ hjN δjJ, n=0 N j=0
(50)

i.e.,

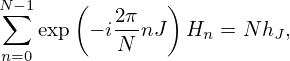N∑−1 ( 2π ) exp − iN-nJ Hn = NhJ, n=0
(51)

which can be solved to give

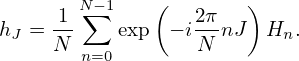N− 1 ( ) hJ = 1-∑ exp − i2πnJ Hn. N n=0 N
(52)

Equation (52) is the inverse DFT.

[prev] [prev-tail] [front] [up]