[next] [prev] [prev-tail] [tail] [up]

6.2 Define DST via DFT

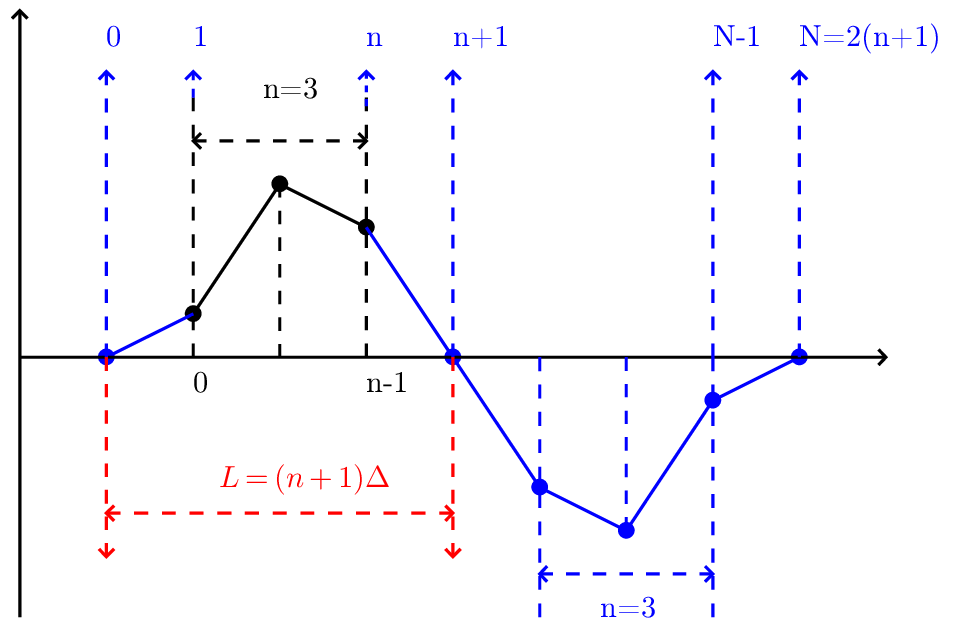
Let us introduce the Discrete Sine Transform (DST) by odd extending a given real number sequence and then using the DFT of the extended data to define DST. There are several slightly different ways of odd extending a given sequence and thus different types of DST. Given a n = 3 real number sequence (a,b,c), one frequently adopted odd extension is (0,a,b,c,0,−a,−b,−c,0). This odd extension is illustrated in Fig. 5.

pict

Figure 5: A frequently used way of defining the odd extension of a sequence of real numbers . The black points are original data (with index 0,1,…,n−1). The blue points are newly introduced, together with the original points, generating an odd periodic sequence of numbers with index 0,1,.,…,N, where N = 2(n+1). The points used in the DFT are 0,1,2,…,N − 1. The period of these data is 2L with L = (n + 1)Δ, where Δ is the spacing between points.

As illustrated in Fig. 5, after the old extension, the total number of points is N + 1 with N = 2(n + 1). Then DFT use the N points with index j = 0,1,…,N − 1 as input. Since the input are real and odd symmetric sequence, the output of this DFT is an odd sequence of purely imaginary numbers. Next, let us prove this. The DFT in this case is given by

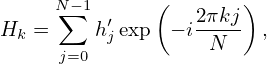N∑−1 ( 2πkj ) Hk = h′jexp − i-N-- , j=0
(58)

where hj′ is the odd extension of the original data hj. For j = 1,2,…,n, the relation between hj′ and hj is given by

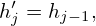′ hj = hj− 1,
(59)

For j = n + 2,…,N − 1, the relation is given by

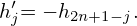′ hj= − h2n+1− j.
(60)

Noting that h0′ = 0 and hn+1′ = 0, then expression (58) is written as

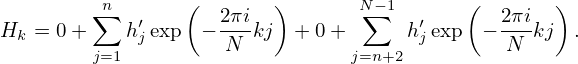∑n ( 2πi ) N∑−1 ( 2πi ) Hk = 0 + h′jexp −-N-kj + 0+ h′jexp − N--kj . j=1 j=n+2
(61)

Using N = 2(n + 1), the above expression is written as

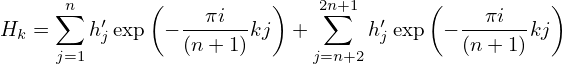n ( ) 2n+1 ( ) H = ∑ h′exp − --πi--kj + ∑ h′ exp − --πi--kj k j=1 j (n + 1) j=n+2 j (n+ 1)
(62)

Using the relations (59) and (60) to replace hj′ by hj, the above expression is written

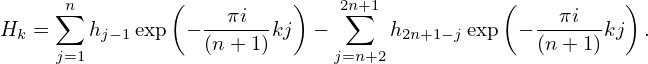( ) ( ) ∑n --πi-- 2∑n+1 --πi-- Hk = hj−1exp − (n + 1)kj − h2n+1−j exp − (n+ 1)kj . j=1 j=n+2
(63)

Change the definition of the dummy index j in the above summation to make it in the conventional range [0 : n − 1], the above expression is written as

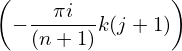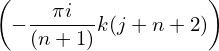Hk = ∑ j=0n−1h j exp( ) − --πi--k(j + 1) (n+ 1)−∑ j=0n−1h n−1−j exp( ) − --πi--k(j + n+ 2) (n + 1).

Defining j′ = n − 1 − j to replace the dummy index in the second summation, the above expression is written as

n∑−1 ( ) ∑0 ( ) Hk = hjexp −--πi--k (j + 1) − hj′ exp − --πi--k(2n + 1− j′) . j=0 (n + 1) j′=n−1 (n + 1) n∑−1 ( ) n∑−1 ( ) = hjexp −--πi--k (j + 1) − hjexp − --πi--k(2n+ 1− j) . j=0 (n + 1) j=0 (n + 1) n∑−1 ( ) n∑−1 ( ) = hjexp −--πi--k (j + 1) − hjexp − --πi--k(− j − 1) . j=0 (n + 1) j=0 (n + 1) n∑−1 ( ) = − 2i hjsin --π---k(j + 1) , (64) j=0 (n + 1)
which is a purely imaginary number. Expression (64) also indicates Hk has the following symmetry
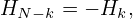HN −k = − Hk,
(65)

i.e. odd symmetry. Therefore only half of the data for Hk with k = 0,1,…,N − 1 need to be stored, namely Hk with k = 0,1,…,N∕2. Expression (64) indicates that H0 and HN∕2 are definitely zero and thus do not need to be stored. Then the remaining data to be stored are Hk with k = 1,2,…N∕2 − 1, i.e. k = 1,2,…,n. Following the convention of making the index of Hk in the range [0 : n− 1], we define Hk′ = Hk+1. Then

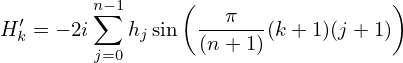n− 1 ( ) H ′= − 2i∑ hjsin ---π--(k +1)(j + 1) k j=0 (n +1)
(66)

with k = 0,1,2,…n− 1, which is the index that we prefer. Finally, the so-called type-I Discrete Sine Transform (DST-I) is defined based on Eq. (66) via

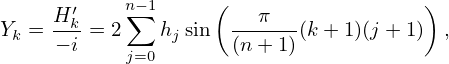H ′ n−∑ 1 ( π ) Yk = −-ki = 2 hjsin (n-+1)(k + 1)(j + 1) , j=0
(67)

with k = 0,1,2,…,n − 1. This is the RODFT00 transform defined in the FFTW library.

[next] [prev] [prev-tail] [front] [up]