[next] [prev] [prev-tail] [tail] [up]

6.3 Reconstruct original function using DST

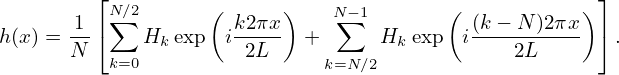
From the above derivation, we know that the DST, Y k, is related to the DFT, Hk, by Y k = Hk+1∕(−i), and thus the meaning of Y k is in principle clear. Next, let us use the DST to reconstruct the original function from which the data are sampled. Since DST is only a special case of DFT, reconstructing the function using DST follows the same procedure used in DFT. In DFT, the function is reconstructed via Eq. (42) (changing to the positive exponent convention), i.e.,

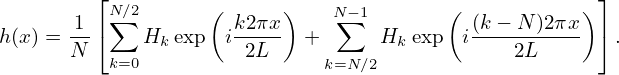⌊N∑ ∕2 ( ) N∑−1 ( ) ⌋ h(x) = 1-⌈ Hk exp ik2πx- + Hk exp i(k-−-N)2πx ⌉. N k=0 2L k=N∕2 2L
(68)

where 2L is the length of the interval in which the samplings hj with j = 0,1,…,N − 1 are made. For our present case, i.e., an odd extension of the original n data, we have N = 2(n + 1) and H0 = 0 and HN∕2 = 0. Then Eq. (68) is written as

[ ( ) ( )] 1- ∑n k2πx- 2∑n+1 (k-−-N-)2πx- h(x) = N 0+ Hk exp i 2L + 0+ Hk exp i 2L . k=1 k=n+2
(69)

Using the odd symmetry of Hk, i.e., Hk = −HN−k, the above expansion is written as

1 [∑n ( k2πx ) 2n∑+1 ( (k − N )2πx )] h(x) = -- Hk exp i---- − HN −kexp i---------- . N k=1 2L k=n+2 2L
(70)

Define k′ = 2n + 2 − k, and note that N = 2(n + 1), then the above expression is written as

[ n ( ) 1 ( )] h(x) = ---1--- ∑ H exp ik2πx- − ∑ H ′ exp i(−-k′)2πx- . 2(n + 1) k=1 k 2L k′=n k 2L
(71)

i.e.,

---1--- ∑n [ ( k2πx-) ( k2πx)] h(x) = 2(n + 1) Hk exp i 2L − exp − i 2L , k=1
(72)

which is simplified as

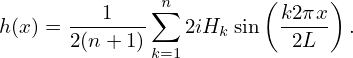1 ∑n ( k2πx ) h (x) = ------- 2iHk sin ----- . 2(n+ 1)k=1 2L
(73)

As a convention, we prefer that the summation index begins from 0 and ends at n − 1. Then expression (73) is written as

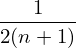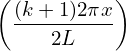
h(x) = ---1--- 2(n +1)∑ k=0n−12iH k+1 sin( ) (k-+-1)2πx- 2L

Using the relation between DST and DFT, i.e., Hk+1 = −iY k, the above equation is written as

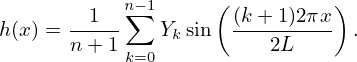-1---n∑−1 ( (k-+-1)2πx-) h(x) = n+ 1 Yksin 2L . k=0
(74)

This is the formula for constructing the continuous function using the DST data. This formula is an expansion over the basis functions sin[(k + 1)πx∕L] with the DST Y k acting as the expansion coefficients. Therefore the direct meaning of the DST, Y k, is that they are the expansion coefficients when using sin(kπx∕L) as the basis functions to approximate a function in the domain [0,L]. From Fig. 5, we know that the interval length L is given by L = (n + 1)Δ, where Δ is the uniform spacing between the original n sampling points.

6.3.1 Inverse DST

Evaluate the function in Eq. (74) at xj = (j + 1)Δ with j = 0,1,…,n − 1, then we obtain

( ) -1---n∑−1 (k-+-1)2π(j +-1)Δ h(xj) = n+ 1 Yksin 2L k=0 ( ) -1---n∑−1 (k-+-1)π(j-+1) = n+ 1 Yksin (n+ 1) . (75) k=0
It can be proved that h(xj) in the above equation exactly recover hj used in defining the DST Y k. Therefore Eq. (75) is the Inverse Discrete Sine Transform.

 

[next] [prev] [prev-tail] [front] [up]