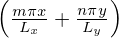 and sin
and sin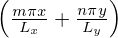 can be readily recovered from
Eqs. (120) and (119). For notation ease, define
can be readily recovered from
Eqs. (120) and (119). For notation ease, define
The formula for expanding a real-valued two-dimensional function G(x,y) in terms of
basis functions cos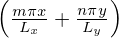 and sin
and sin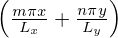 can be readily recovered from
Eqs. (120) and (119). For notation ease, define
can be readily recovered from
Eqs. (120) and (119). For notation ease, define
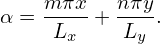 | (121) |
Then Eq. (120) is written as
![∑∞ ∞∑
G(x,y) = cmn [cosα + isinα ]
m= −∞ n= −∞ ( )
∑∞ ∞∑ ---1--∫ Ly ∫ Lx
= 4LxLy − Ly −Lx G (x,y)cos αdxdy [cosα + isinα]
m= −∞ n= −∞ ( ∫ ∫ )
∑∞ ∞∑ ---1-- Ly Lx
+ 4LxLy − Ly −Lx G (x,y)sinαdxdy [− icosα + sin α],
m= −∞ n= −∞](fourier_analysis134x.png)
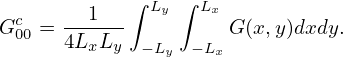 | (124) |
and the other coefficients given by
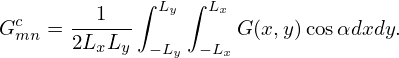 | (125) |
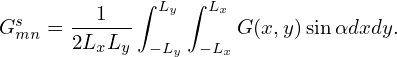 | (126) |
Here the range of m is reduced to [0 : +∞]. In this case, we have an edge case, G00c, that needs special treatment. We see that allowing the index runing from −∞ to +∞ has the advantage of that there are no edge cases that needs special treatment.