2D real-valued Fourier series derived directly from real-valued trigonometric functions expansion– to be deleted, because there is an easier way to do this, as is given by the above section

C.2 2D real-valued Fourier series derived directly from real-valued trigonometric functions expansion– to be deleted, because there is an easier way to do this, as is given by the above section

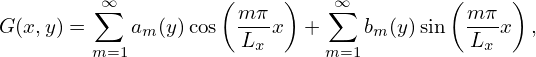
We see that the extension of Fourier series from one-dimension case to two-dimension case is straightforward when expressed in terms of the complex exponential function e^inπx∕L. However, if we use sin(mπx∕L_x), cos(mπx∕L_x), sin(nπy∕L_y), and cos(nπy∕L_y) as basis functions, the derivation of the two-dimensional Fourier series of G(x,y) is a little complicated (product-to-sum trigonometric identities are involved to simplify the results). Let’s see the derivation. A two-dimensional function G(x,y) can be ﬁrst expanded as Fourier series about x,

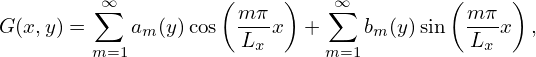∞∑ ( m π ) ∑∞ ( mπ ) G (x,y) = am (y)cos ---x + bm (y)sin ---x , m=1 Lx m=1 Lx

(127)

(the zero-frequency component is dropped, will take it back later) and then the two coeﬃcients a_m(y) and b_m(y) can be further expanded as Fourier series about y,

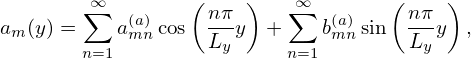∞∑ ( ) ∑∞ ( ) am (y) = a(am)n cos nπ-y + b(man)sin nπ-y , n=1 Ly n=1 Ly

(128)

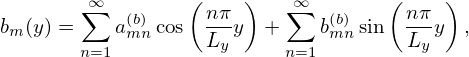∞ ( ) ∞ ( ) ∑ (b) nπ- ∑ (b) nπ- bm (y) = n=1amncos Lyy + n=1bmn sin Ly y ,

(129)

(the zero-frequency component is dropped, will take it back later) Substituting Eq. (128) and (129) into Eq. (127), we obtain

[ ] ∞∑ ∑∞ (a) ( nπ ) ∑∞ (a) ( nπ ) ( mπ ) G (x,y) = amn cos Lyy + bmn sin Lyy cos Lx-x m=1[n=1 ( ) n=1 ( ) ] ( ) ∞∑ ∑∞ (b) nπ- ∑∞ (b) nπ- mπ- + amn cos Lyy + bmn sin Lyy sin Lx x(1.30) m=1 n=1 n=1

Using the product-to-sum trigonometric identities, equation (130) is written

[ ( ) ( )] 1 ∞∑ ∑∞ (a) m-π nπ- m-π nπ- G (x,y) = 2 amn cos Lx x + Ly y + cos Lx x− Lyy m=∞1 n=∞1 [ ( ) ( ) ] + 1 ∑ ∑ b(a) sin m-πx + nπy + sin m-πx − nπy 2m=1 n=1 mn Lx Ly Lx Ly ∞∑ ∑∞ [ ( ) ( )] + 1 a(mb)n sin m-πx + nπy − sin m-πx − nπ-y 2m=1 n=1 Lx Ly Lx Ly 1 ∞∑ ∑∞ (b) [ (m π nπ ) ( mπ n π )] + 2 bmn cos L--x − L-y − cos L--x+ L--y m=1 n=1 x y x y

which can be organized as

∑∞ ∑∞ ( ) G(x,y) = 1[a(man)− b(mb)n]cos mπ-x+ n-πy m=1n=1 2 Lx Ly ∑∞ ∑∞ 1 ( mπ nπ ) + 2[b(man)+ a(mb)n]sin L--x+ L--y m=1n=1 ( x y ) ∑∞ ∑∞ 1 (a) (b) mπ- n-π + 2[amn + bmn]cos Lx x− Lyy m=∞1n=∞1 ( ) + ∑ ∑ 1[b(a)− a(b)]sin mπ-x− nπ-y (131) m=1n=1 2 mn mn Lx Ly

The coeﬃcients appearing above are written as

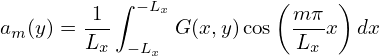( ) -1-∫ −Lx m-π am (y) = Lx −L G (x,y)cos Lx x dx x

(132)

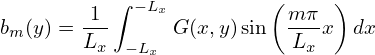1 ∫ −Lx ( mπ ) bm (y) = Lx G (x,y)sin Lx-x dx −Lx

(133)

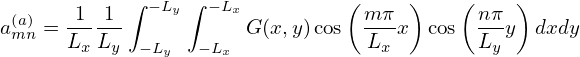∫ ∫ ( ) ( ) a(a)= -1--1- −Ly −Lx G(x,y)cos m-πx cos nπy dxdy mn Lx Ly −Ly −Lx Lx Ly

(134)

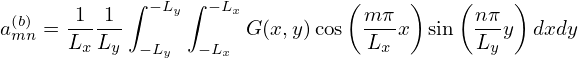∫ ∫ ( ) ( ) a(b)= -1--1- −Ly −Lx G(x,y)cos m-π x sin nπy dxdy mn Lx Ly −Ly − Lx Lx Ly

(135)

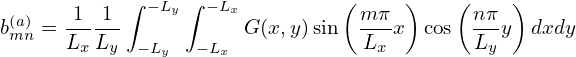∫ −L ∫ −L ( ) ( ) b(a)= -1--1- y x G(x,y)sin m-πx cos nπy dxdy mn Lx Ly −Ly −Lx Lx Ly

(136)

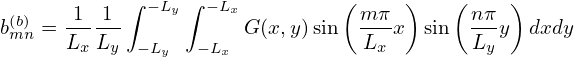∫ −Ly∫ −Lx ( ) ( ) b(mbn)= 1--1- G(x,y)sin m-πx sin n-πy dxdy LxLy −Ly − Lx Lx Ly

(137)

Noting that b_m,−n^(b) = −b_m,n^(b), and a_m,−n^(b) = −a_m,n^(b) and sin(0) = 0, then Eq. (131) can be written as

∑∞ ∑∞ ( ) G (x,y) = 1[a(man)− b(bm)n]cos mπ-x+ nπ-y m=1n=− ∞ 2 Lx Ly ∑∞ ∑∞ 1 (m π nπ ) + -[b(man)+ a(bm)n]sin ---x + ---y . (138) m=1n=− ∞ 2 Lx Ly

The coeﬃcients can be further written as

cmn ≡ 1[a(man)− b(bm)n] 2 ∫ ∫ [ ( ) ( ) ( ) ( ) ] = 1-1-1-- −Ly −LxG (x,y) cos m-πx cos nπ-y − sin mπ-x sin nπy dxdy 2Lx Ly − Ly −Lx Lx Ly Lx Ly ∫ −Ly ∫ −Lx ( ) = 1-1-1-- G (x,y)cos m-πx+ nπy dxdy. (139) 2Lx Ly − Ly −Lx Lx Ly

1 smn ≡ -[b(man)+ a(bm)n] 2 ∫ − Ly∫ −Lx [ ( ) ( ) ( ) ( )] = 1-1-1-- G (x,y) sin mπ-x cos nπ-y + cos m-πx sin nπ-y dxdy 2Lx Ly −Ly −Lx Lx Ly Lx Ly 1 1 1 ∫ − Ly∫ −Lx ( mπ n π ) = 2Lx-Ly- G (x,y)sin Lx-x+ -Lyy dxdy. (140) −Ly −Lx

Then comes the drudgery to handle the special cases of m = 0 and/or n = 0. The ﬁnal results are identical to Eqs. (123)-(126). This kind of derivation is also discussed in my notes on mega code.

[prev] [prev-tail] [front] [up]