2D Fourier series

C 2D Fourier series

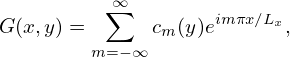
Compared with Eq. (1) that uses the trigonometric functions, Fourier series (15) and (16), which is expressed in terms of the complex exponential function e^inπx∕L, is more compact. The convenience introduced by the complex exponential function is more obvious when we deal with multiple-dimensional cases. For example, a two-dimensional function G(x,y) can be expanded as Fourier series about x,

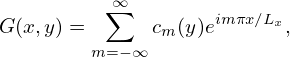∞ G (x,y) = ∑ c (y)eimπx∕Lx, m=−∞ m

(117)

where 2L_x is the period of G in x direction. The expansion coeﬃcients c_m(y) can be further expanded as Fourier series about y,

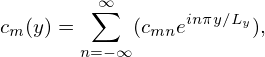∞∑ inπy∕L cm (y) = (cmne y), n=−∞

(118)

where 2L_y is the period of G in y direction, and the coeﬃcients c_mn is given by

∫ [ ∫ ] -1-- Ly -1-- Lx − im πx∕Lx −inπy∕Ly cmn = 2Ly −Ly 2Lx −Lx G(x,y)e dx e dy. ∫ Ly∫ Lx = --1--- G(x,y)e−im πx∕Lx−inπy∕Lydxdy. (119) 4LxLy −Ly − Lx

Using Eq. (118) in Eq. (117), we obtain

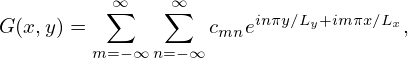∞∑ ∑∞ inπy∕Ly+imπx∕Lx G(x,y) = cmne , m= −∞ n=−∞

(120)

Equations (120) and (119) give the two-dimensional Fourier series of G(x,y).

C.1 For 2D real-valued functions
C.2 2D real-valued Fourier series derived directly from real-valued trigonometric functions expansion– to be deleted, because there is an easier way to do this, as is given by the above section

[next] [prev] [prev-tail] [front] [up]