8 Heat diffusivity

A general conservation law for a scalar quantity K can be written as

(287)

where S is a source term, and Q is the flux, which can often be divided into two terms: the diffusive term and convective term, i.e.,

(288)

where χ is called the diffusivity, u is the flow velocity that transports K.

[If u = 0 and χ is constant, then Eq. (287) without the source term reduces to the following parabolic equation:

(289)

which is often called diffusion equation.]

Next, let us neglect the convection, i.e., set u = 0. For the case of energy diffusion, K is the kinetic energy density, i.e., K = 3n_sT_s∕2, where ns is the number density and T_s is the temperature. Assuming that n is constant in space, then the diffusivity χ in Eq. (288) can be written as

(290)

In studying tokamak energy transport, it is the radial component that is of interest. The energy radial diffusivity (or conductivity) χ is defined as

(291)

where ⟨…⟩ is the flux-surface average, and Q is the radial energy flux defined by

(292)

where μ = mv_⊥²∕(2B₀), V_G0 is the equilibrium drift, V_G1 is the drift perturbation, δf is the distribution function perturbation. The flux contributed by the equilibrium drift (i.e., linear flux) is usually small and neglected [The equilibrium drift has only n = 0 component. The fulx-surface averaging will make all the n≠0 δf components multiplied by the equilibrium be zero. Only n = 0 component (zonal component) of δf, multiplied by the equilibrium drift can give nonzero flux. For this flux to be significant, the zonal component usually needs to be very strong.]

The perturbed distribution function contains a term: 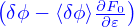, i.e., the polarization term. This term’s contribution to the heat flux is usually small and is ignored (confirmed by Ye Lei).

Equation (291) indicates that the unit of χ in SI units is m²∕s.

Bohm and gyroBohm scaling

For a species s, the gyro-Bohm energy diffusivity is defined by

(293)

whereas the Bohm diffusivity is defined by

(294)

where s is the species label, c_s = 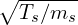is the thermal speed, ρ_s = c_s∕Ω_s is the thermal Larmor radius, Ω_s = Bq_s∕m_s is the cyclotron frequency, L_s is the radial gradient scale length of temperature or density of species s. Because L_s evolves in δf gyrokinetic simulations without source terms, some autors prefer to replace L_s in the above definition by the minor radius of the LCFS, a.

Comparing Eqs. (293) and (294), we know that the Bohm diffusivity is L_s∕ρ_s times larger than the gyroBohm one. The energy diffusitivity observed in gyrokinetic simulations usuall is much samller than χ_B and is often of the same order of χ_GB.

The Bohm diffusitivity can also be written as:

(295)

which is independent of the machine size, and the gyro-Bohm diffusitivity can be written as

(296)

where L_s is replaced by the minor radius of the LCFS, a. The gyro-Bohm diffusitivity decreases with increasing machine size. The gyro-Bohm diffusivity is proportional to 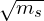, which means heavier isotops have larger diffusivity if the satisfy the gyro-Bohm scaling.