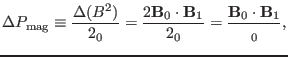Next we consider the radial component of the momentum equation. Taking scalar
product of the momentum equation with
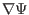 , we obtain
, we obtain
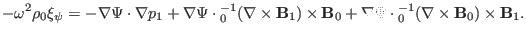 |
(106) |
After some algebra (the details are given in Sec. (9.5)), Eq.
(106) is written
where
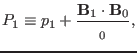 |
(108) |
and
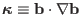 is the
magnetic field curvature with
is the
magnetic field curvature with
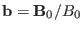 the unit vector
along equilibrium magnetic field. Equation (107) agrees with Eq.
(17) in Cheng's paper[3]. In passing, let us examine the
physical meaning of
the unit vector
along equilibrium magnetic field. Equation (107) agrees with Eq.
(17) in Cheng's paper[3]. In passing, let us examine the
physical meaning of 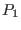 defined by (108). In linear approximation,
we have
defined by (108). In linear approximation,
we have
This indicates the perturbation in the square of the magnetic strength is
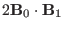 . Therefore, the perturbation in magnetic
pressure is written
. Therefore, the perturbation in magnetic
pressure is written
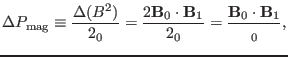 |
(110) |
which indicate 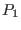 defined by Eq. (108) is the total perturbation
in the thermal and magnetic pressure.
defined by Eq. (108) is the total perturbation
in the thermal and magnetic pressure.
yj
2015-09-04
![]() , we obtain
, we obtain