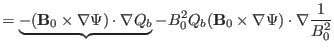The
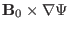 component of the linearized momentum
equation is written
component of the linearized momentum
equation is written
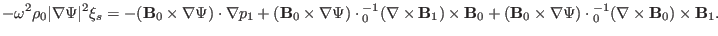 |
(111) |
The last term of Eq. (111) is written
Using Eq. (335), i.e.,
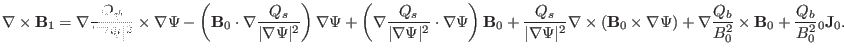 |
(113) |
the second last term on the right-hand side of Eq. (111) is written
The term
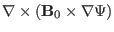 in the above
equation is written as
in the above
equation is written as
Gathering terms involving 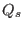 , excluding the first term, in expression
(115) gives
, excluding the first term, in expression
(115) gives
which can be proved to be zero (refer to Sec. 9.6 for the proof).
Gathering terms involving 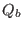 in expression (115) gives
in expression (115) gives
It can be proved that the second term of the above expression is equal to
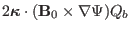 (refer to
Sec. 9.9 for details). Thus, from Eq. (114), we obtain
(refer to
Sec. 9.9 for details). Thus, from Eq. (114), we obtain
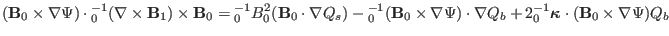 |
(117) |
Using Eqs. (112) and (117) in Eq. (111) yields
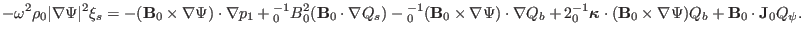 |
(118) |
Using
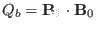 , the above equation can be
arranged as
, the above equation can be
arranged as
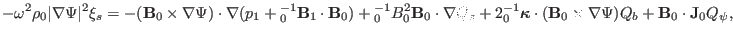 |
(119) |
which agrees with Eq. (18) in Cheng's paper[3].
yj
2015-09-04
![]() component of the linearized momentum
equation is written
component of the linearized momentum
equation is written
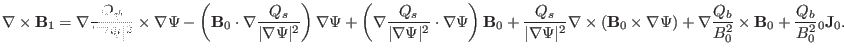
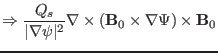
![$\displaystyle \frac{Q_s}{\vert \nabla \Psi \vert^2} [-
(\mathbf{B}_0 \cdot \nab...
...times \mathbf{B}_0 + \nabla \Psi
\cdot \nabla \mathbf{B}_0 \times \mathbf{B}_0]$](img310.png)
![$\displaystyle (\mathbf{B}_0 \times \nabla \Psi) \cdot \left[ Q_s \left( \mathbf...
...{B}_0 + (\nabla \Psi \cdot \nabla \mathbf{B}_0) \times
\mathbf{B}_0] \right], $](img312.png)
![$\displaystyle (\mathbf{B}_0 \times \nabla \Psi) \cdot \left[ - B^2_0 \nabla
\frac{Q_b}{B^2_0} \right]$](img314.png)
![$\displaystyle = (\mathbf{B}_0 \times \nabla \Psi) \cdot \left[ - B^2_0 Q_b \nabla
\frac{1}{B^2_0} - \nabla Q_b \right]$](img315.png)