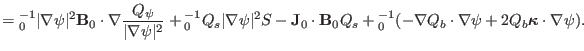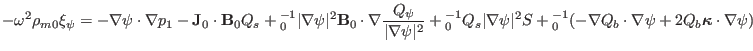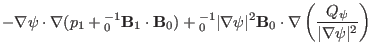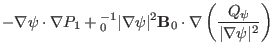proof: The derivation of Eq. (107)
Using Eq. (65), we obtain
Using this, the second term on the right-hand side of Eq. (106) is
written
The first term of Eq. (336) is written
The last equality is due to
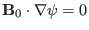 . The second
term of Eq. (336) is written
. The second
term of Eq. (336) is written
The last equality is due to that the coefficients before 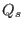 , i.e.,
, i.e.,
is equal to
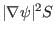 (refer to Sec. 9.7 for the proof).
The third term of Eq. (336) is written
(refer to Sec. 9.7 for the proof).
The third term of Eq. (336) is written
Using Eqs. (337)-(339) in Eq. (336) yields
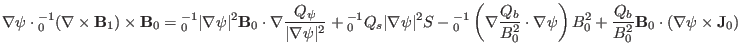 |
(340) |
Now we calculate the
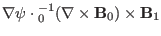 term appearing in Eq. (106),
which can be written as
term appearing in Eq. (106),
which can be written as
Gathering the terms involving 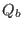 in Eqs. (340) and
(341), we obtain
in Eqs. (340) and
(341), we obtain
The second term of Eq. (342) is written
The last term of Eq. (342) is written
The terms in Eqs. (343) and (344) exactly cancel each
other. Thus the expression in (342) now reduces to
![$\displaystyle {\textmu}_0^{- 1} \left\{ - \nabla Q_b \cdot \nabla \psi + 2 \fra...
...{B^2_0} \mathbf{B}_0 \cdot [- (\mathbf{B}_0 \cdot \nabla) \nabla \psi] \right\}$](img967.png) |
(345) |
Noting that
the expression (345) is further written as
where
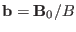 is the unit vector along the direction of
equilibrium magnetic field, and
is the unit vector along the direction of
equilibrium magnetic field, and
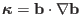 is the magnetic field curvature. Using these results, we obtain
is the magnetic field curvature. Using these results, we obtain
| |
|
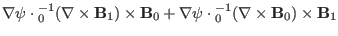 |
|
| |
|
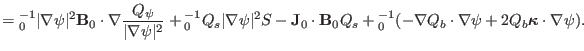 |
(347) |
Using the above results, the radial component equation
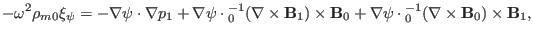 |
(348) |
is written as
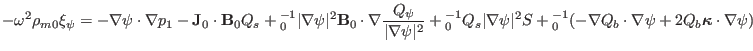 |
(349) |
which can be arranged in the form
Define
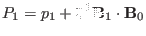 , the
above equation is written as
, the
above equation is written as
which is identical with Eq. (107).
yj
2015-09-04
![$\displaystyle \frac{1}{\vert \nabla \psi \vert^2} \mathbf{B}_0 \cdot [(\mathbf{...
...la)
\nabla \psi - (\nabla \psi \cdot \nabla) \mathbf{B}_0] \times \nabla \psi
$](img944.png)
![$\displaystyle {\textmu}_0^{- 1} \left\{ - \nabla Q_b \cdot \nabla \psi + 2
\frac{Q_b}{B^2} [\mathbf{B}_0 \cdot \nabla \mathbf{B}_0] \cdot \nabla \psi
\right\}$](img971.png)
![$\displaystyle ={\textmu}_0^{- 1} \left\{ - \nabla Q_b \cdot \nabla \psi + 2 Q_b...
... \left(
\frac{\mathbf{B}_0}{B_0} B_0 \right) \right] \cdot \nabla \psi \right\}$](img972.png)
![$\displaystyle ={\textmu}_0^{- 1} \left\{ - \nabla Q_b \cdot \nabla \psi + 2 Q_b...
...ac{1}{B_0} [\mathbf{b} \cdot \nabla (\mathbf{b}B_0)] \cdot \nabla \psi
\right\}$](img973.png)