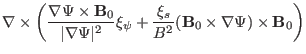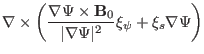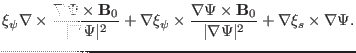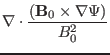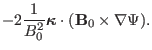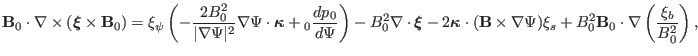The component of the induction equation in the direction of
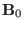 is
written as
is
written as
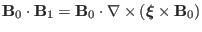 |
(88) |
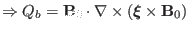 |
(89) |
The term on right-hand side of the above equation is written as
Using this, the right-hand side of Eq. (89) is written as
Before we try to simplify the above equation, we derive the expression for the
divergence of
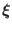 , which is written as
, which is written as
It can be proved that the fourth term of the above equation can be written as
(refer to (9.8) for the proof)
Then Eq. (93) is written as
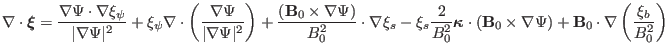 |
(95) |
Eq. (95) agrees with Eq. (23) in Cheng's paper, but a 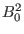 factor
is missed in the fourth term of Cheng's equation[3]. Using Eq.
(95), Eq. (92) is written as
factor
is missed in the fourth term of Cheng's equation[3]. Using Eq.
(95), Eq. (92) is written as
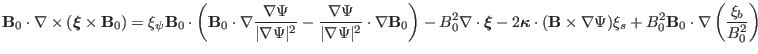 |
(96) |
It can be proved that
 |
(97) |
(Refer to Sec. 9.10 for the proof.) Then Eq. (96) is
written as
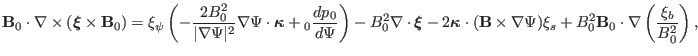 |
(98) |
and the component of the induction equation in the direction of
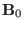 [Eq. (89)] is finally written as
[Eq. (89)] is finally written as
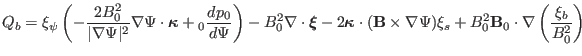 |
(99) |
Eq. (99) agrees with Eq. (22) in Cheng's paper[3].
yj
2015-09-04
![]() is
written as
is
written as