Surface operator acting on perturbation

Next, consider the calculation of the surface operators acting on the above perturbation. Using Eq. (168), we obtain

$$\mathbf{B}_0 \cdot \nabla (a G) = - \Psi' \mathcal{J}^{- 1} \sum_{n = - \infty}^{\infty} \sum_{m = ... ...a}{\partial \theta} + i (m - n q) a \right] G_{n m} e^{i (m \theta - n \zeta)},$$ (172)

where $a = a (\psi, \theta)$ is a known function that is independent of $\zeta$. Similarly, we have

$$\mathbf{B}_0 \cdot \nabla (a\mathbf{B}_0 \cdot \nabla G)$$

$$= - \Psi' \mathbf{B}_0 \cdot \nabla \left[ a\mathcal{J}^{- 1} \sum_{m, n} i (m - n q) G_{n m} (\psi) e^{i (m \theta - n \zeta)} \right]$$

$$= (\Psi')^2 \mathcal{J}^{- 1} \sum_{m, n} \left[ \frac{\partial}{\p... ...\mathcal{J}^{- 1} \right] i (m - n q) G_{n m} (\psi) e^{i (m \theta - n \zeta)}$$

$$= (\Psi')^2 \sum_{m, n} \left[ i (m - n q) \mathcal{J}^{- 1} \frac{... ...- n q)^2 a\mathcal{J}^{- 2} \right] G_{n m} (\psi) e^{i (m \theta - n \zeta)} .$$ (173)

Using Eq. (169), we obtain

$$\left( \frac{\mathbf{B}_0 \times \nabla \Psi}{B_0^2} \right) \cdot \nabla G$$

$$= \left( 1 + \Psi' g q \frac{\mathcal{J}^{- 1}}{B_0^2} \right) (- i... ...hcal{J}^{- 1}}{B_0^2} \sum_{m, n} i m G_{n m} (\psi) e^{i (m \theta - n \zeta)}$$

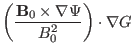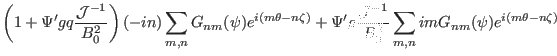$$= \sum_{m, n} \left[ i (m - n q) \Psi' g \frac{\mathcal{J}^{- 1}}{B_0^2} - i n \right] G_{n m} (\psi) e^{i (m \theta - n \zeta)} .$$ (174)