The elements of matrix 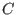 ,
, 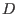 ,
, 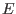 , and
, and 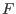 are two dimensional differential
operators about
are two dimensional differential
operators about
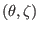 , which can be called surface differential
operators. As discussed above, we use Fourier expansion to treat the
differential with respect to
, which can be called surface differential
operators. As discussed above, we use Fourier expansion to treat the
differential with respect to 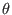 and
and 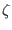 . In this method, we need to
take inner product between different Fourier harmonics. Noting this, we
recognize that it is useful to define the following inner product operator:
. In this method, we need to
take inner product between different Fourier harmonics. Noting this, we
recognize that it is useful to define the following inner product operator:
where 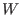 is a surface differential operator of the following form
is a surface differential operator of the following form
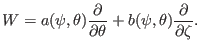 |
(175) |
Because both of the coefficients in expression (175) are independent
of 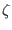 , it is ready to see that, for
, it is ready to see that, for 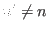 ,
,
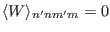 . This indicates that
. This indicates that 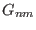 with different
with different 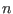 are decoupled
with each other.
are decoupled
with each other.
For notation ease,
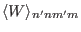 is denoted by
is denoted by
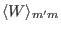 when
when 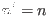 , i.e.,
, i.e.,
[For the special case that 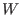 is an algebra operator
is an algebra operator
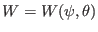 ,
equation (5) can be reduced to
,
equation (5) can be reduced to
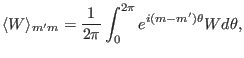 |
(176) |
where
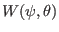 is independent of
is independent of 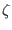 because, as we will see
below,
because, as we will see
below, 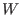 is determined by equilibrium quantities (for example,
is determined by equilibrium quantities (for example,
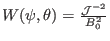 ), which is axisymetrical.
Expression (176) is a Fourier integration over the interval
), which is axisymetrical.
Expression (176) is a Fourier integration over the interval
![$ [0, 2
\pi]$](img451.png) , which can be efficiently calculated by using the FFT algorithm (details
are given in Chapter 13.9 of Ref. [5]).] After using the
Fourier harmonics expansion and taking the inner product, every element of the
matrices
, which can be efficiently calculated by using the FFT algorithm (details
are given in Chapter 13.9 of Ref. [5]).] After using the
Fourier harmonics expansion and taking the inner product, every element of the
matrices 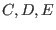 , and
, and 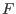 becomes a
becomes a
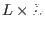 matrix, where
matrix, where 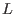 is the
total number of the Fourier harmonics included in the expansion. Taking the
matrix
is the
total number of the Fourier harmonics included in the expansion. Taking the
matrix
 as an example, it is discretized as
as an example, it is discretized as
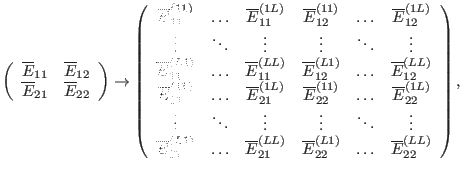 |
(177) |
where
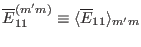 ,
,
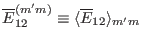 ,
,
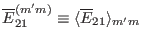 ,
,
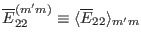 . Next, let us derive the expressions of
. Next, let us derive the expressions of
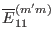 ,
,
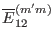 ,
,
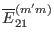 ,
,
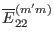 . The goal of he derivation is to perform the
surface differential operators so that all the inner products take the form of
the Fourier integration given by Eq. (176). For the convenience of
reference, the expression of matrix
. The goal of he derivation is to perform the
surface differential operators so that all the inner products take the form of
the Fourier integration given by Eq. (176). For the convenience of
reference, the expression of matrix
 is repeated here:
is repeated here:
Then
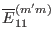 is written as
is written as
Making use of Eq. (173), equation (178) is written as
![$\displaystyle \overline{E}_{11}^{m' m} = - \frac{2 \overline{\omega}^2 \overlin...
...rt \nabla \Psi \vert^2 \mathcal{J}^{- 2}}{B_0^2} \right\rangle_{m' m} \right] .$](img469.png) |
(179) |
Note that all the operators within the inner operator
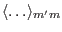 of the above equation are algebra operators. Therefore the
calculation of the inner product
of the above equation are algebra operators. Therefore the
calculation of the inner product
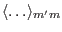 reduces to
the calculation of the Fourier integration (176), which can be
efficiently calculated by using the FFT algorithm (it is thus implemented in
GTAW). Similarly, the discrete form of the other matrix elements are written
respectively as:
reduces to
the calculation of the Fourier integration (176), which can be
efficiently calculated by using the FFT algorithm (it is thus implemented in
GTAW). Similarly, the discrete form of the other matrix elements are written
respectively as:
Next, consider the discrete form of the normalized 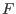 matrix, which is given
by
matrix, which is given
by
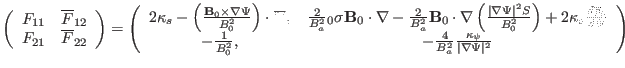 |
(183) |
Using Eqs. (139) and (159), we obtain
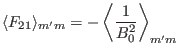 |
(186) |
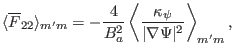 |
(187) |
Next, we derive the discrete form of matrix 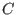 and
and 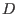 . Before doing this, we
examine matrix equation (161), which can be written as
. Before doing this, we
examine matrix equation (161), which can be written as
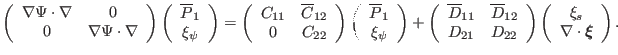 |
(188) |
Using the expression of the operator
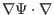 , i.e.,
, i.e.,
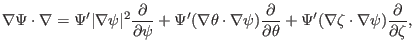 |
(189) |
equation (188) is written as
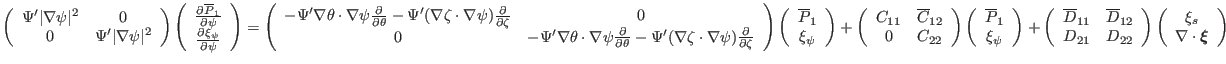 |
(190) |
Define the first matrix on the r.h.s of the above equation as
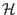 ,
then
,
then
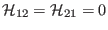 , and
, and
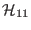 and
and
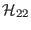 are given by
are given by
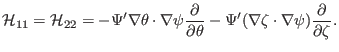 |
(191) |
Then
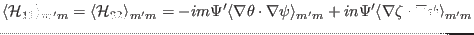 |
(192) |
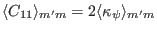 |
(193) |
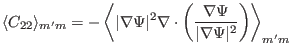 |
(194) |
The formula for calculating the right-hand side of Eq. (194) is
given in Sec. 8.6.
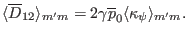 |
(196) |
Subsections
yj
2015-09-04
![]() ,
, ![]() ,
, ![]() , and
, and ![]() are two dimensional differential
operators about
are two dimensional differential
operators about
![]() , which can be called surface differential
operators. As discussed above, we use Fourier expansion to treat the
differential with respect to
, which can be called surface differential
operators. As discussed above, we use Fourier expansion to treat the
differential with respect to ![]() and
and ![]() . In this method, we need to
take inner product between different Fourier harmonics. Noting this, we
recognize that it is useful to define the following inner product operator:
. In this method, we need to
take inner product between different Fourier harmonics. Noting this, we
recognize that it is useful to define the following inner product operator:
![$\displaystyle \langle W \rangle_{n' n m' m} \equiv \frac{1}{(2 \pi)^2} \int_0^{...
... [i (n' \zeta - m' \theta)] W \exp [i (m \theta - n
\zeta)] d \theta d \zeta, $](img437.png)
![]() is denoted by
is denoted by
![]() when
when ![]() , i.e.,
, i.e.,
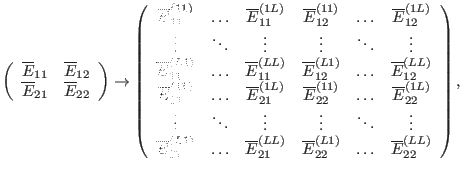
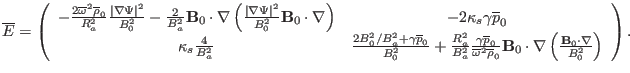
![$\displaystyle \overline{E}_{11}^{m' m} = - \frac{2 \overline{\omega}^2 \overlin...
...rt \nabla \Psi \vert^2 \mathcal{J}^{- 2}}{B_0^2} \right\rangle_{m' m} \right] .$](img469.png)
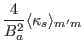
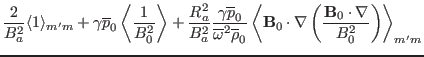
![$\displaystyle \frac{2}{B_a^2} \langle 1 \rangle_{m' m} + \gamma \overline{p}_0
...
... q)^2 \left\langle \frac{\mathcal{J}^{-
2}}{B_0^2} \right\rangle_{m' m} \right]$](img480.png)
![]() matrix, which is given
by
matrix, which is given
by
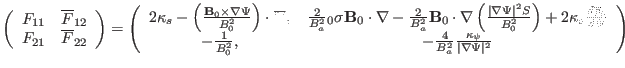
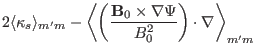
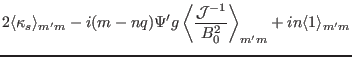


![$\displaystyle - \Psi' \frac{2}{B_a^2} i (m - n q) \langle {\textmu}_0 \sigma
\m...
... m} \right] + 2 \frac{d \overline{p}_0}{d \Psi}
\langle \kappa_s \rangle_{m' m}$](img490.png)
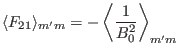
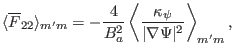
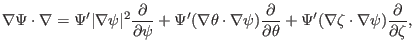
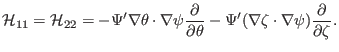
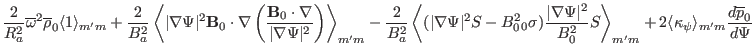
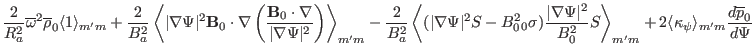
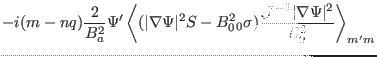
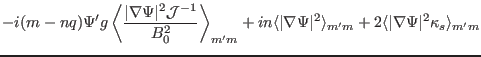
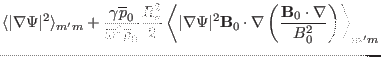
![$\displaystyle \langle \vert \nabla \Psi \vert^2 \rangle_{m' m} + (\Psi')^2 \fra...
...vert \nabla \Psi
\vert^2 \mathcal{J}^{- 2}}{B_0^2} \right\rangle_{m' m} \right]$](img513.png)