Next: Eigenmodes Up: Linearized ideal MHD equation Previous: Fourier transformation in time
In dealing with eigenmodes, we ususally encounter discrete frequency
perturbations, i.e., ![]() is periodic function of
is periodic function of ![]() so that they contian
only discrete frequency components. In this case, the inverse Fourier
transformtion in Eq. (31) is replaced by the Fourier series, i.e.,
so that they contian
only discrete frequency components. In this case, the inverse Fourier
transformtion in Eq. (31) is replaced by the Fourier series, i.e.,
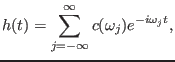 |
(38) |
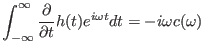 |
(40) |
 |
(41) |
yj 2015-09-04