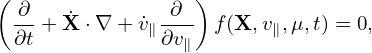
Frimain-Chen equation was obtained by first transforming to the guiding-center coordinates and then using the classical perturbation expansion for the distribution function (to separate gyro-phase independent part form the gyro-phase dependent one). Note that the guiding-center transform does not involve the perturbed field.
The modern form of the nonlinear gyrokinetic equation is in the total-f form. This way of deriving the gyrokinetic equation is to use coordinate transforms to eliminate gyro-phase dependence of the total distribution function (rather than splitting the distribution function itself) and thus obtain an equation for the resulting gyro-phase independent distribution function (called gyro-center distribution function). The coordinate transform involves the perturbed fields besides the equilibrium field.
The resulting equation for the gyro-center distribution function is given by (see Baojian’s paper)
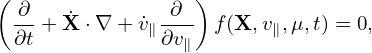 | (420) |
where
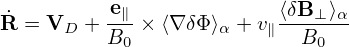 | (421) |
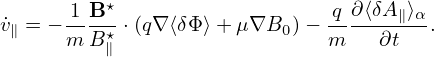 | (422) |
Here the independent variables are gyro-center position X, magnetic moment μ and parallel velocity v∥.
The gyro-phase dependence of the particle distribution can be recovered by the inverse transformation of the transformation used before. The pull-back transformation (inverse gyro-center transform) gives rise to the polarization density term. (phase-space-Lagrangian Lie perturbation method (Littlejohn, 1982a, 1983), I need to read these two papers.).
The learning curve of modern Lie tansform gyrokinetic is steep: the name Lie transform itself is already very scaring.
To derive the Frieman-Chen equation, you just need some patience.