Derivation of Eq. (123), not ﬁnished

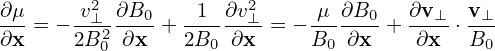
From the deﬁnition of μ, we obtain

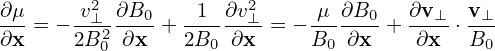2 2 ∂μ-= − v⊥--∂B0-+ -1--∂v⊥-= −-μ-∂B0-+ ∂v-⊥ ⋅ v⊥- ∂x 2B20 ∂x 2B0 ∂x B0 ∂x ∂x B0

(417)

Using

∂v⊥-= ∂[v-−-v∥e∥]-= − v ∂e∥ − ∂v∥e , ∂x ∂x ∥ ∂x ∂x ∥

(418)

expression (417) is written as

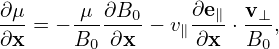∂μ μ ∂B ∂e v ---= − -----0 − v∥--∥⋅-⊥-, ∂x B0 ∂x ∂x B0

(419)

which agrees with Eq. (10) in Frieman-Chen’s paper[3].

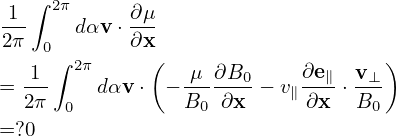
1 ∫ 2π ∂μ --- dαv ⋅--- 2π 0∫ 2π ∂x( ) = -1- dαv ⋅ − -μ-∂B0-− v ∂e∥⋅ v⊥- 2π 0 B0 ∂x ∥∂x B0 =?0

∫ 2π [ ( )] -1- dαv ⋅ v× -∂- e∥ ⋅ ∂-δG0 2π 0 ∂x Ω ∂X =

Using the fact that δG₀ is independent of α, the left-hand side of Eq. (123) is written as

⟨v ⋅[∫λB1 + λB2{][δG0 ⟩α ] } = -1- 2πdαv ⋅ v × -∂-(e∥) ⋅ ∂δG0-+ ∂μ-∂δG0-+ ∂α-∂δG0 2π 0 ∂x Ω ∂X ∂x ∂μ ∂x ∂α 1 ∫ 2π {[ ∂ (e∥) ] ∂δG0 ∂μ ∂δG0 } = 2π- dαv ⋅ v × ∂x- Ω- ⋅-∂X--+ ∂x--∂μ-- 0