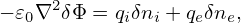
Poisson’s equation is written as
|
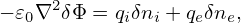| (221) |
where −𝜀0∇2δΦ is called the space-charge term. Since we consider modes with k∥≪ k⊥, the space-charge term is approximated as ∇2δΦ ≡∇⊥2δΦ + ∇∥2δΦ ≈∇⊥2δΦ. Then Eq. (221) is written as
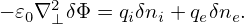 | (222) |
This approximation eliminates the parallel plasma oscillation from the system. The perpendicular plasma oscillations seem to be only partially eliminated in the system consisting of gyrokinetic ions and drift-kinetic electrons. There are the so-called ΩH modes (also called electrostatic shear Alfven wave) that appear in the gyrokinetic system which have some similarity with the plasma oscillations but with a much smaller frequency, ΩH ∼ (k∥∕k⊥)(λD∕ρs)ωpe.
Using expression (203), the perturbed number density δn is written as
where the blue term is approximately zero for isotropic F0 and this term is usually dropped in simulations that assume isotropic F0 and approximate δA as δA∥e∥. The red term in expression (223) is the so-called the polarization density np, i.e.,
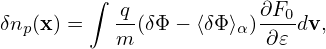 | (224) |
which has an explicit dependence on δΦ and is usually moved to the left hand of Poisson’s equation when constructing the numerical solver of the Poisson equation, i.e., equation (222) is written as
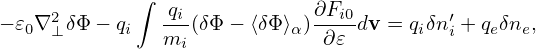 | (225) |
where δni′ = δni −δnpi = ∫ δhidv, which is evaluated by using Monte-Carlo markers. Since some parts depending on δΦ are moved from the right-hand side to the left-hand side of the field equation, numerical solvers (for δΦ) based on the left-hand side of Eq. (225) probably behaves better than the one that is based on the left-hand side of Eq. (222), i.e., −𝜀0∇⊥2δΦ.
The polarization density is part of the perturbed density that is extracted from the source term and moved to the left-hand side of the Poisson equation. The polarization density will be evaluated without using Monte-Carlo markers, whereas the remained density on the right-hand side will be evaluated using Mote-Carlo markers. The two different methods of evaluating two parts of the total perturbed density can possibly introduce significant errors if the two terms are expected to cancel each other and give a small quantity that is much smaller than either of the two terms. This is one pitfall for PIC simulations that extract some parts from the source term and move them to the left-hand side. To remedy this, rather than directly moving a part of the distribution function to the left-hand side, we subtract an (approximate) analytic expression from both sides of Eq. (222). The analytical expressions on both sides are evaluated based on grid values of perturbed electromagnetic fields and are independent of makers. All the original parts of the distribution functions are kept on the right-hand side and are still evaluated by using markers, which hopefully avoids the possible cancellation problem. This strategy is often called a cancellation scheme. Since unknown perturbed electromagnetic fields appear on the right-hand side, iteration is needed to solve the field equation.
Note that two things appear here: What motivates us to move parts of the distribution function to the left? It is the goal of hopefully making the left-hand side matrix more well-behaved (such as good condition number, etc.) Why do we need the cancellation scheme? Because we want to avoid the numerical inaccuracy that appears when large terms cancels each other. Note that iteration is needed when the cancellation scheme is used because the right-hand side explicitly contains unknown electromagnetic fields.
It turns out that the cancellation scheme is not necessary for Eq. (225), but for the field solver for Ampere’s equation (discussed later), this cancellation scheme is necessary in order to obtain stable results.
![∫
δn = δFdv
∫ ∫ [ ] ∫ [ ]
= δhdv+ q-(δΦ − ⟨δΦ⟩α)∂F0- dv+ -q⟨v ⋅δA⟩α∂F0- dv, (223)
m ∂𝜀 m ∂𝜀](nonlinear_gyrokinetic_equation263x.png)