[next] [prev] [prev-tail] [tail] [up]

5.3 Summary of split of the distribution function

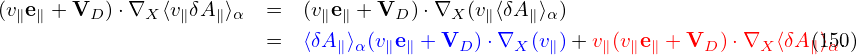
In the above, the perturbed part of the distribution function, δF, is split at least three times in order to (1) simplify the gyrokinetic equation by splitting out the adiabatic response and (2) eliminate the time derivatives, ∂δϕ∕∂t and (3) ∂δA∕∂t, on the right-hand. To avoid confusion, I summarize the split of the distribution function here. The total distribution function F is split as

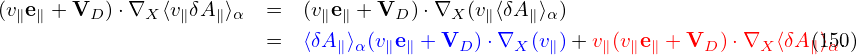F = F0 +δF,
(150)

where F0 is the equilibrium distribution function and δF is the perturbed part of the total distribution function. δF is further split as

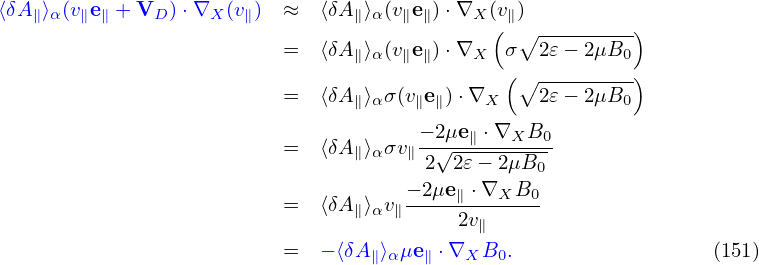q ∂F q ∂F δF = δh + --(δΦ− ⟨δΦ⟩α)--0-+ --⟨v⋅δA ⟩α --0, m ∂𝜀 m ∂𝜀
(151)

where δh satisfies the gyrokinetic equation (142) or (149). In Eq. (151), the red term gives rise to the so-called polarization density (discussed in Sec. 5.6). The analytic dependence of this term on δΦ is utilized in solving the Poisson equation. The blue term also has an analytic dependence on δA, which, however, will cause numerical problems in particle simulations if it is utilized in solving the Ampere equation (the so-called “cancellation problem” in gyrokinetic simulations).

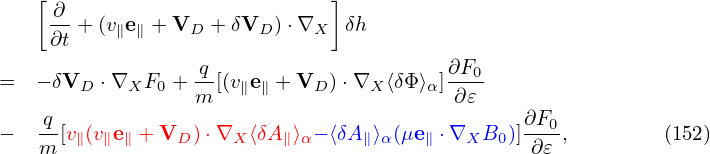Velocity space moment of q m-⟨v ⋅ δA⟩α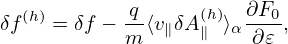∂∂F𝜀0

Consider the approximation δA ≈ δA∥e∥, then the blue term in Eq. (151) is written as

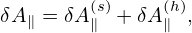q-⟨vδA ⟩ ∂F0. m ∥ ∥α ∂𝜀
(152)

Notice that v∥ can be taken out of the gyro-averaging. Then the above equation is written

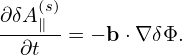q- ∂F0- m v∥⟨δA ∥⟩α ∂𝜀 .
(153)

If we neglect the FLR effect, then the above expression is written

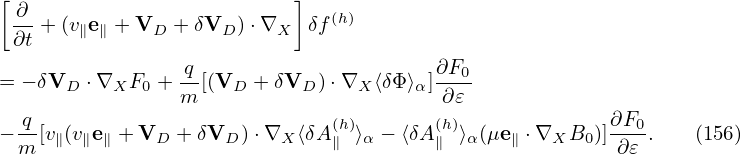-qv δA ∂F0-. m ∥ ∥ ∂𝜀
(154)

The zeroth order moment (number density) is then written as

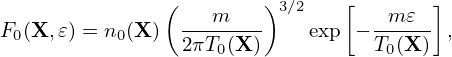∫ q- ∂F0- δn = m δA∥ v∥∂ 𝜀 dv,
(155)

which is zero if F0 is Maxwellian.

Next, consider the parallel current carried by distribution (154), which is written

q2 ∫ 2∂F0 δj∥ = m-δA ∥ v∥-∂𝜀-dv.
(156)

If F0 is a Maxwellian distribution given by

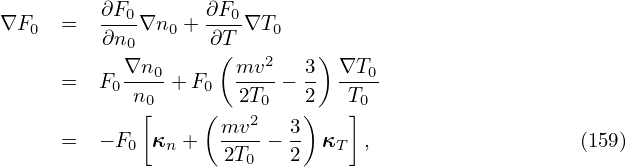( ) ( -m--)3∕2 mv2- F0 = n0 2πT exp − 2T .
(157)

then

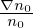∂F0-= − m-F0. ∂𝜀 T
(158)

Then expression (156) is written

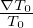2 ( )3∕2 ∫ ( 2) δj∥ = − q-n0 -m-- δA ∥ v2∥exp − mv-- dv. T 2πT 2T
(159)

Working in the spherical coordinates, then v∥ = v cos𝜃 and dv = v2 sin𝜃dvd𝜃dϕ. Then expression (159) is written

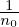
( ) ∫ ( ) δj = − q2n -m-- 3∕2δA v2cos2𝜃exp − mv2- v2sin𝜃dvd𝜃dϕ ∥ T 0 2πT ∥ 2T q2 ( m )3∕2 4π∫ 4 ( mv2 ) = − T-n0 2πT- δA ∥3-- v exp −-2T- dv (160) 2 ( )3 ∕2 ∫ = − q-n0 1- 2TδA 4π- x4exp(− x2)dx T π m ∥3 q2 ( 1)3 ∕2 2T 4π3√ π- = − T-n0 π- m-δA ∥3---8- 2 = − q-n0δA∥. (161) m
Ampere’s Law
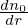− ∇2⊥ δA(∥n+1)= μ0(δJ (n||i+1)+ δJ(|n|e+1)).
(162)

The parallel currents are given by

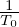∫ q2 ∂F δJ(n||i+1)= δJ|′|i(δϕ(n),δA(∥n)) + (v(∥n+1))2-i-⟨δA (n∥+1)⟩α--i0dv, mi ∂𝜀
(163)

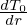(n) ∫ (n+1) q2 (n+1) ∂Fe0 δJ||e = δJ′||e(δϕ(n),δA ∥ )+ (v∥ )2-e⟨δA ∥ ⟩α ----dv, me ∂𝜀
(164)

where δJ∥i′ and δJ∥e′ is the parallel current carried by the distribution function δh in Eq. (151), which are updated from the value at the nth time step to the (n + 1)th time step using an explicit scheme and therefore does not depends on the field at the (n + 1)th step. The blue terms in Eqs. (163) and (164) depend on the field at the (n + 1)th step and thus need to be moved to the left-hand side of Ampere’s law (162) if we want to solve this equation by direct methods. In this case, equation (162) is written as

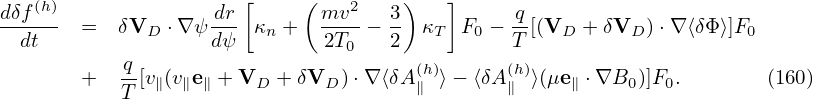
∫ 2 − ∇2⊥δA(∥n+1)− μ0 (v(n∥+1))2 qi⟨δA(∥n+1)⟩α ∂Fi0-dv ∫ mi ∂ 𝜀 − μ (v(n+1))2 q2e⟨δA (n+1)⟩ ∂Fe0dv. 0 ∥ me ∥ α ∂𝜀 = μ (δJ ′(δϕ (n),δA(n))+ δJ′ (δϕ(n),δA(n))) (165) 0 ∥i ∥ ||e ∥
However the gyro-averaging in the blue terms can not be evaluated analytically. If evaluated numerically using markers, the corresponding matrix will depends on markers and thus needs to be re-constructed and inverted each time-step, which is computationally expensive. Therefore we go back to Eq. (162) and try to solve it using iterative methods. However, it is found numerically that directly using Eq. (162) as an iterative scheme is usually divergent. To obtain a convergent iterative scheme, we need to have an approximate form for the blue terms, which is independent of markers and so that it is easy to construct its matrix, and then subtract this approximate form from both sides. After doing this, the iterative scheme has better chance to be convergent. An approximate form is that derived by neglecting the FLR effect given in Sec. 5.3. Using this, the iterative scheme for solving Eq. (162) is written as
( ) − ∇2 δA(n+1) − μ − q2in δA(n+1) − q2en δA(n+1) ⊥ ∥ 0 mi i0 ∥ me e0 ∥ = μ [δJ′(δϕ(n),δA(n))+ δJ′(δϕ(n),δA (n))] 0∫ ∥i ∥ ||e ∥ + μ (v(n+1))2-qi2⟨δA(n+1)⟩ ∂Fi0dv 0 ∥ mi ∥ α ∂𝜀 ∫ (n+1)2-q2e (n+1) ∂Fe0 + μ0 (v∥ )me ⟨δA∥ ⟩α ∂𝜀 dv ( q2 q2 ) − μ0 − -ini0δA(∥n+1)− -e-ne0δA (n∥+1) . (166) mi me
In the drift-kinetic limit (i.e., neglecting the FLR effect), the blue and red terms on the right-hand side of the above equation cancel each other exactly. Even in this case, it is found numerically that these terms need to be retained and the blue terms are evaluated using markers. Otherwise, numerical inaccuracy can give numerical instabilities, which is the so-called cancellation problem. The explanation for this is as follows. The blue terms are part of the current. The remained part of the current is computed by using Monte-Carlo integration over markers. If the blue terms are evaluated analytically, rather than using Monte-Carlo integration over markers, then the cancellation between this analytical part and Monte-Carlo part can have large error (assume that there are two large contribution that have opposite signs in the two parts) because the two parts are evaluated using different methods and thus have different accuracy, which makes the cancellation less accurate.

The blue terms are sometimes called “adiabatic current”. The red terms are approximation to the “adiabatic current” obtained by neglecting the FLR effect. Because the ion adiabatic current is less than the electron adiabatic current by a factor of me∕mi, its accuracy is not important, and is approximated by the drift-kinetic limit in GEM. And the cancellation error is not a problem and hence can be neglected. In this case, equation (166) is simplified as

( ) − ∇2 δA(n+1) − μ − q2in δA(n+1) − q2en δA(n+1) ⊥ ∥ 0 mi i0 ∥ me e0 ∥ = μ [δJ′(δϕ(n),δA(n))+ δJ′(δϕ(n),δA (n))] 0∫ ∥i ∥ ||e ∥ + μ (v(n+1))2 q2e⟨δA(n+1)⟩ ∂Fe0dv 0 ∥ me ∥ α ∂𝜀 ( q2e- (n+1)) − μ0 − me ne0δA ∥ . (167)

[next] [prev] [prev-tail] [front] [up]