The perturbed distribution function is decomposed as given by Eq. (151), i.e.,
 | (168) |
where the term in blue is the so-called adiabatic response, which depends on the gyro-angle. Recall that the red term ⟨δΦ⟩α, which is independent of the gyro-angle, is introduced in order to eliminate the time derivative ∂⟨δΦ⟩α∕∂t term on the right-hand side of the original Frieman-Chen gyrokinetic equation.
The so-called generalized split-weight scheme corresponds to going back to the original Frieman-Chen gyrokinetic equation by introducing another ⟨δΦ⟩α term with a free small parameter 𝜖g. Specifically, δh in the above is split as
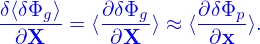 | (169) |
(If 𝜀g = 1, then the two ⟨δΦ⟩α terms in Eq. (168) and (169) cancel each other.) Substituting this expression into Eq. (143), we obtain the following equation for δhs:
Noting that ∂F0∕∂t = 0, e∥⋅∇F0 = 0, ∇F0 ∼ O(λ1)F0, we find that the third line of the above equation is of order O(λ3) and thus can be dropped. Moving the second line to the right-hand side, the above equation is written asFor the special case of 𝜖g = 1 (the default and most used case in GEM code, Yang Chen said 𝜖g < 1 cases are sometimes not accurate, so he gave up using it since 2009), equation (171) can be simplified as:
where two VG ⋅⟨δΦ⟩α terms cancel each other. Because the v∥E∥ term is one of the factors that make kinetic electron simulations difficult, eliminating VG ⋅⟨δΦ⟩α term may be beneficial for obtaining stable algorithms.For 𝜖g = 1, δF is written as
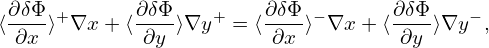
Equation (172) actually goes back to the original Frieman-Chen equation. The only difference is
that 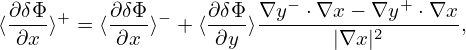 ⟨v ⋅δA⟩α
⟨v ⋅δA⟩α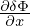 is further split from the perturbed distribution function. Considering this, equation
(172) can also be obtained from the original Frieman-Chen equation (133) by writing δG0
as
is further split from the perturbed distribution function. Considering this, equation
(172) can also be obtained from the original Frieman-Chen equation (133) by writing δG0
as
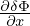 | (174) |
In this case, δF is written as
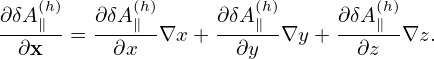 | (175) |
Substituting expression (174) into equation (133), we obtain the following equation for δhs:
Noting that ∂F0∕∂t = 0, e∥⋅∇F0 = 0, ∇F0 ∼ O(λ1)F0, we find that the third line of the above equation is of order O(λ3) and thus can be dropped. Moving the second line to the right-hand side, the above equation is written as which agrees with Eq. (172).In GEM, the split weight method is used only for electrons and the ∂⟨δΦ⟩α∕∂t is approximated by ∂δΦ∕∂t and this term is obtained from the vorticity equation (rather than from an implicit iteration).