[next] [tail] [up]

E.1 Expression of δB⊥ in terms of δA

Note that

δB ⊥ = ∇ × δA − (e∥ ⋅∇ × δA )e∥ = ∇ × (δA ⊥ + δA∥e∥)− [e∥ ⋅∇ × (δA ⊥ +δA ∥e∥)]e∥ (282)
Correct to order O(λ), δB⊥ in the above equation is written as (e∥ vector can be considered as constant because its spatial gradient combined with δA will give terms of O(λ2), which are neglected)
δB⊥ ≈ ∇ × δA ⊥ + ∇ δA∥ × e∥ − [e∥ ⋅∇ × δA ⊥ + e∥ ⋅(∇ δA∥ ×e∥)]e∥ (283) = ∇ × δA ⊥ + ∇ δA∥ × e∥ − (e∥ ⋅∇ × δA ⊥)e∥ (284)
Using local cylindrical coordinates (r,ϕ,z) with z being along the local direction of B0, and two components of A⊥ being Ar and Aϕ, then ∇× A⊥ is written as
( ∂δAϕ ) (∂δAr ) 1 [ ∂ ∂δAr ] ∇ × δA ⊥ = − -∂z-- er + -∂z-- eϕ + r ∂r(rδAϕ)− -∂-ϕ- e∥.
(285)

Note that the parallel gradient operator ∇∥≡ e∥⋅∇ = ∂∕∂z acting on the the perturbed quantities will result in quantities of order O(λ2). Retaining terms of order up to O(λ), equation (285) is written as

1 [ ∂ ∂ δAr ] ∇ ×δA ⊥ ≈ r ∂r(rδAϕ)− -∂-ϕ- e∥,
(286)

i.e., only the parallel component survive, which exactly cancels the last term in Eq. (284), i.e., equation (284) is reduced to

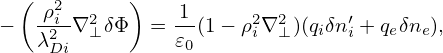δB⊥ = ∇ δA ∥ × e∥.
(287)

[next] [front] [up]